 図 1-2-1 |
わたしたちは,「力」,「運動量」,「エネルギー」というみっつの存在が,それぞれなにであり,それぞれがたがいとどのような関係にあるかを,高校物理の学習に役立つ範囲で見ていきます.学校の教科書は,時間を無駄にしないように,それらの点を簡潔に記述しています.一方,わたしたちは,なるべく道草を食いながらそれらを見ていきましょう.そのあとで読みなおせば,教科書の記述が的確であると分かるでしょう.
「力」,「運動量」,「エネルギー」のうち,科学の歴史に最初に現れたものは「運動量」です.まず,「運動量」の素朴な姿を見ましょう.
 図 1-2-1 |
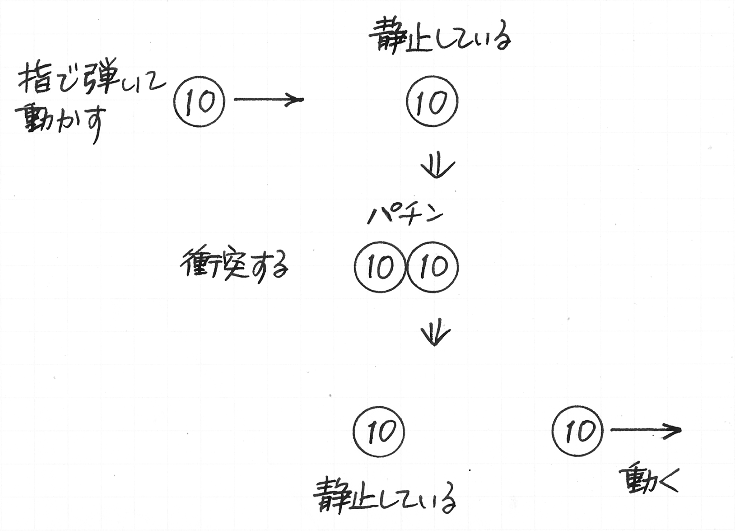
なるべくでこぼこのない机に,二枚の 10 円玉を,すこし間を開けて並べます.そして,一方の 10 円玉を指で弾いて動かし,それを静止している 10 円玉にぶつけます.うまくぶつけると,動いていた 10 円玉が止まり,その瞬間に,静止していた 10 円玉が動きだします.
あえて非科学的に表現するならば,それはまるで,一方の 10 円玉に潜んでいた「勢い」が,衝突をきっかけにして,他方の 10 円玉に乗りうつったかのようです.
では,次のふたつの現象で,一方の「勢い」が他方に乗りうつったとわたしたちは説明できるでしょうか.
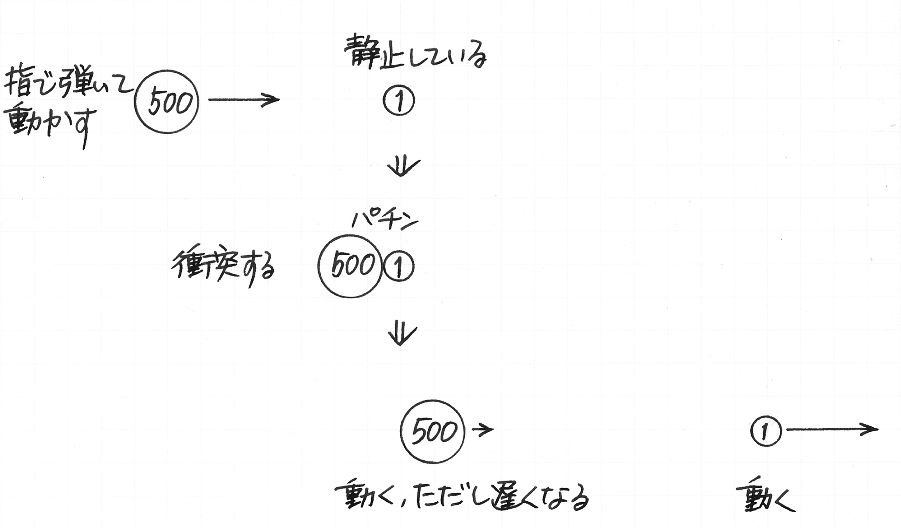 図 1-2-2 |
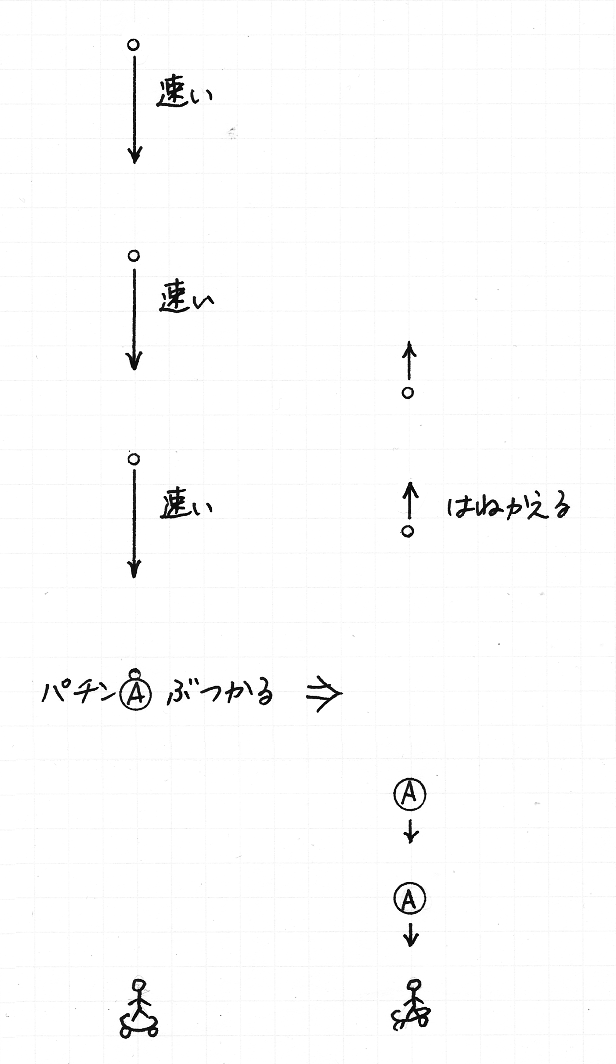
異なる種類の硬貨──たとえば 1 円玉と 500 円玉と──を,すこし間を開けて机に並べます.そして,大きいほうの 500 円玉を指で弾いて動かし,それを静止している 1 円玉にぶつけます.この場合,1 円玉が動きだしたあと,500 円玉が遅くなりながらも動きつづけるという現象が見られます.もしそれを「勢い」のしわざとして説明しようとすると,はじめ 500 円玉には大勢の「勢いたち」がいて,その一部が 1 円玉に乗りうつり,その他の「勢いたち」は 500 円玉に居残ったとでも言わなければならないことでしょう.
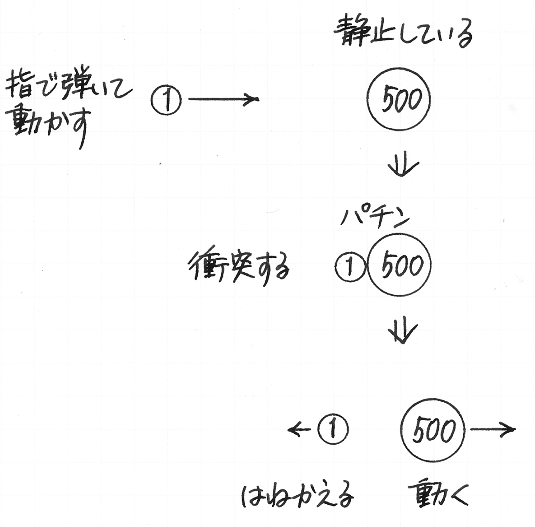 図 1-2-3 |
反対に,小さいほうの 1 円玉を動かして,それを 500 円玉にぶつける場合,500 円玉が動きだすと同時に,1 円玉は,はねかえって,衝突前と逆向きに動くという現象が見られます.もしそれを「勢いたち」のしわざとして説明しようとすると,衝突後に 1 円玉に居残った「勢いたち」がなぜ逆向きに動くかを説明するのに苦労することでしょう.
そこで,わたしたちは,非科学的な「勢い」といった存在の代わりに,「相対速度」と「物質の分割」という考えかたにもとづいて,これらの運動の変化を説明できるかどうか試しましょう.そのためにまず,「相対速度」と「物質の分割」とについて触れる必要があります.
17 世紀,ガリレオ・ガリレイが暮らしていたヴェネツィアには港があり,そこに多くの帆船が出入りしていました.帆船には,帆を張るための支柱があり,その最頂部で船員が遠くを見張っていました.
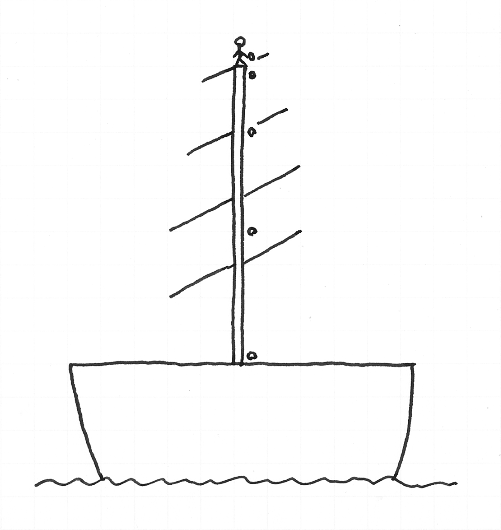 図 1-3-1 |
船が港で錨泊しているとき,見張りの船員が支柱のてっぺんからうっかり石を落としたとします.強い風が吹いていないかぎり,石はまっすぐに落ちて,支柱のふもとあたりにぶつかるでしょう.石は,落下しているあいだ,だんだん速くなります.そのことは実験によって確かめられます.
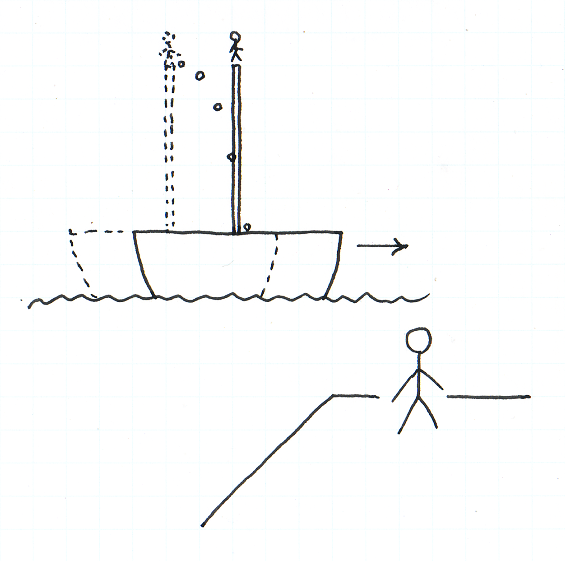 図 1-3-2 | 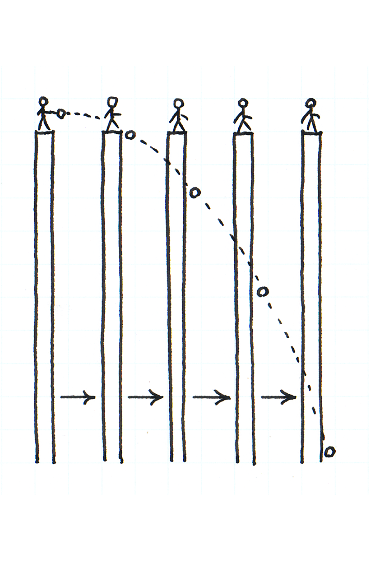 図 1-3-3 |
波が穏やかな晴れの日には,船に乗っている人々にとって,船が進んでいるのか停まっているのか分からないくらい静かであることがあります.もし見張りの船員が,船が前進しているのに気づかないまま,石を落としたとすると,それはどのように落下するでしょうか.石は,船が停まっている場合と同じように,支柱のふもとあたりにぶつかります.そのことは実験によって確かめられます.
その場合,石は「まっすぐに」落ちていると言っていいでしょうか.落下する石を陸上で見ているひとがいるとします.石は,船員の手元から落ちて,支柱のふもとあたりにぶつかります.石が落下しているあいだに船がいくらか前進するので,石が落下しはじめるときの支柱の位置と,ぶつかるときの位置とは,陸上で見ているひとにとって異なります.陸上のひとにとって,石は,曲線に沿って落ちているように見えます.一方,見張りの船員にとって,石は,自分の足元の方向にまっすぐ落下しているように見えます.
このように,同一の運動が,あるひとにはまっすぐであるように見え,別のひとには曲線に沿っているように見えることがあります.運動を記述するさいには,どこで見たかを明確にしておかないと,意味を成さないことがあります.
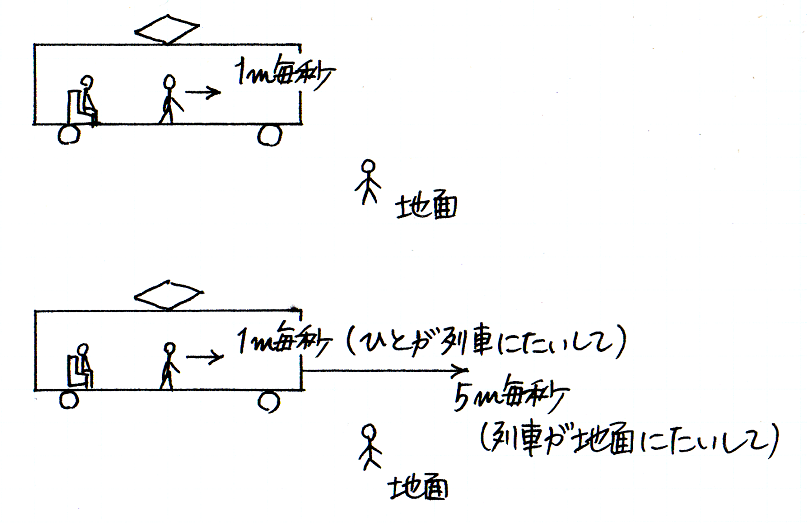 図 1-3-4 |
もうひとつの例を見ておきましょう.静止している列車のなかを,1 m 毎秒の速さで歩いているひとがいるとします.そのひとの速さは,同じ列車で座っているひとが見ても,地面に立っているひとが見ても,1 m 毎秒です.
次に,列車が地面にたいして 5 m 毎秒の速さで前進しているとします.そして,ひとが,列車が進むのと同じ方向に,列車にたいして 1 m 毎秒の速さで前進しているとします.そのひとの速さは,同じ列車で座っているひとが見ると 1 m 毎秒ですが,地面に立っているひとが見ると 6 m 毎秒です.
このとき,次の関係が成立します:
| ( | 地面にたいする ひとの速度 |
) | = | ( | 列車にたいする ひとの速度 |
) | + | ( | 地面にたいする 列車の速度 |
). |
列車にたいするひとの速度を,「列車にたいするひとの相対速度」ということがあります.日常で「列車の速度」という表現は,ほとんどの場合,「地面にたいする列車の相対速度」の意味です.もし地面が不動であるならば,わざわざ「地面にたいする」と言う必要はありませんが,わたしたちはのちに,地球が太陽のまわりを動く運動について考察します.それにそなえて,なにが動いても使える表現を工夫しておく必要があります.わたしたちもまた,地球の運動などを考えなくていい場面では,「地球にたいする」という表現を省略することがあるでしょう.しかし,厳密に言うならば,すべての「速度」は,なんらかのものにたいする「相対速度」です.
わたしたちの当面の考察にとって,相対速度の話題は,この程度で十分です.しかし,あえて寄道をしておきましょう.前進する船と落下する石とについて『天文対話』(1632)で論じたガリレオは,地動説を信じていました.地動説は,地球を含む惑星すべてが太陽のまわりを公転しているという学説です.それは今日当然として受けいれられていますが,ガリレオの時代に,それを唱えた者は死刑に処せられるおそれがありました.キリスト教を篤く信仰していた人々の一部は,神が人の姿で降臨した地球が宇宙の中心でないという考えに反発しました.権威あるローマ法王が,地球に乗って太陽を回る小さい存在であるという考えに,我慢ならない人々もいました.彼らのなかに,地動説に反論を試みる人々がいました.もし地球がたえず動いているのであれば,そこに住む人々はなぜ地球から振りおとされないのか,と.
船と石とについてのガリレオの考察は,その反論にたいする回答の意味をもっていました.前進している船での石の運動は,船上の人々が見れば,船が静止している場合の運動と変わるところがありません.同じように,たとえ地球が太陽のまわりを動いていたとしても,地球上の人々が見れば,地球上の物体の運動は,もし地球が静止している場合の運動と変わるところがありません.船が前進していると気づいていない船員が船から振りおとされないのと同じように,地球が動いていると気づいていない人々が地球から振りおとされることはありません.そのことは,ガリレオにとって命懸けの主張であり,『天文対話』は出版後まもなく禁書となり,彼は異端審問を受けて,地動説を捨てるように命じられました.
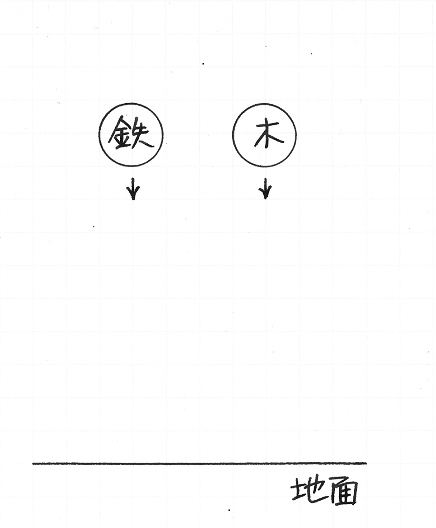 図 1-4-1 | 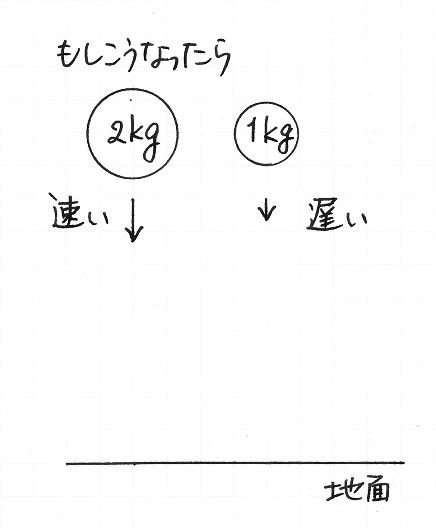 図 1-4-2 |
こんどは,重いものは軽いものより速く落ちるかどうかを考えましょう.鉄と木とで球をひとつずつ作るとします.材質が異なるので,ふたつの球の重さは異なります.それらふたつの球を,等しい高さから同時に手放すと,どちらが先に地面にぶつかるでしょうか.あるいは,ふたつは同時に着地するでしょうか.答えは,同時に着地する,です.そのことは,実験で確かめられます.
けれど,そんなことくらい実験をするまでもなく分かると,『新科学対話』(1638)でガリレオ・ガリレイは述べています.重さが異なるふたつの球が同じように落下することは,次のように説明されます.かりに,1 kg の球より 2 kg の球のほうが速く落ちるとします.すると,ひょうたん形にくびれた 2 kg の物体は,どのように落下するでしょうか.また,糸でつながれたふたつの 1 kg の球は,どのように落下するでしょうか.それらは,1 kg の物体として落下するのか,2 kg の物体として落下するのか.かりに重さによって物体の落下のしかたが異なるならば,ひとがなにをひとつのまとまりと見なすかによって,物体の落下のしかたが異なることでしょう.そんなことは起こりそうにありません.現実には,重いものも軽いものも同じように落下するので,ひょうたん形の物体や糸でつながれた物体は,他の物体と同じように落下します.
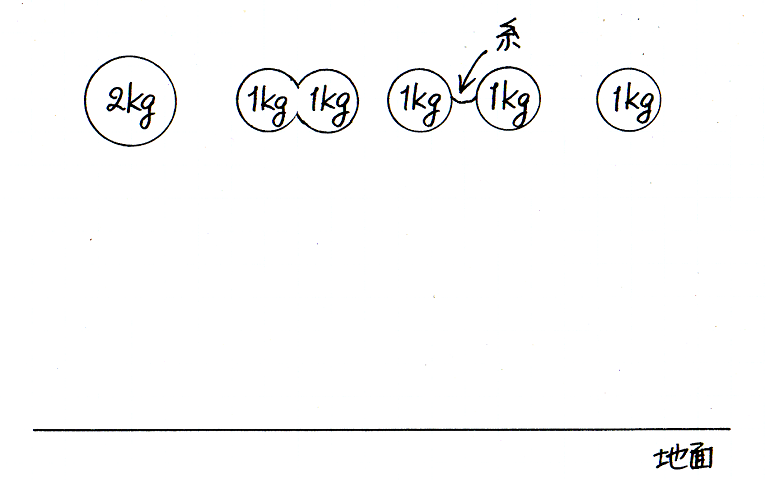 図 1-4-3 | 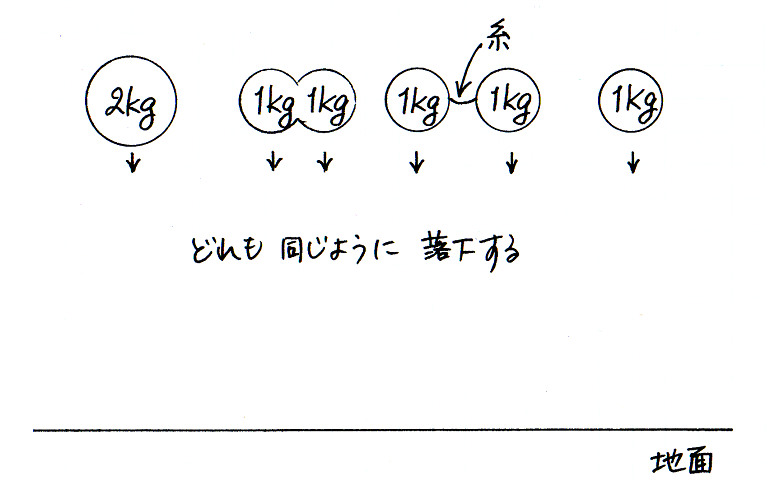 図 1-4-4 |
わたしたちは,物体の運動について考察するさい,物体をひとまとまりのものとして捉えてもいいし,物体の部分に注目してもかまいません.もし物体全体の運動を説明しようとする理論が,全体と調和している部分の運動を説明できないならば,その理論はおそらく誤っているでしょう.
相対速度について考えたり,物体の部分の運動について考えたりすることは,ひとつの運動を複数の観点から理解するということです.わたしたちは,複数の観点から,硬貨の衝突について再考しましょう.
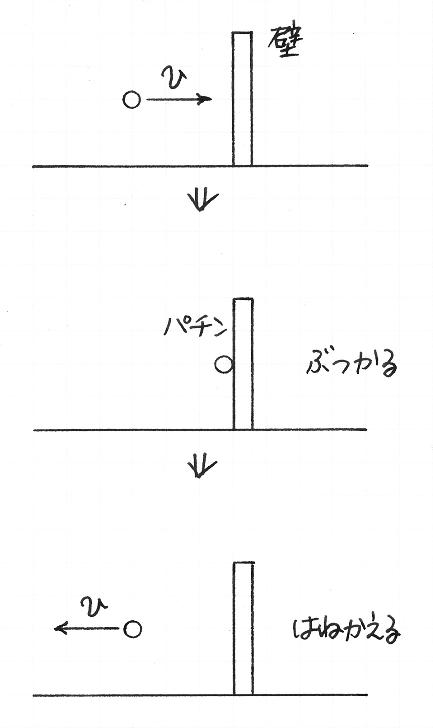 図 1-5-1 |
まず,ボールが壁にぶつかってはねかえる現象を見ましょう.地面にたいする速さ v で飛んでいるボールが,壁にぶつかって,もと来たほうへ,地面にたいする速さ v で戻っていくとします.壁のところで静止しているひとにとって,このボールは,まず速さ v で近づいてきて,はねかえったあと,速さ v で遠ざかります.
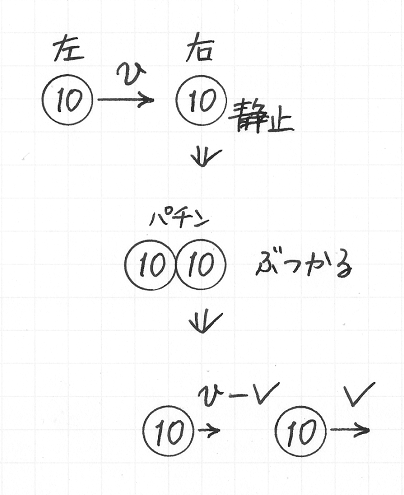 図 1-5-2 |
次に,二枚の 10 円玉が衝突する現象について再考します.左の 10 円玉が,地面にたいする速さ v で動いていて,右にある,地面にたいして静止している 10 円玉にぶつかるとします.その衝突をきっかけにして,右の 10 円玉が,地面にたいする速さ V で動きだし,左の 10 円玉は減速するとします.左の 10 円玉がどれくらい減速するか,わたしたちには分かりませんが,右の 10 円玉の速さが 0 から V に増えたので,左の 10 円玉の速さは,それと同じだけ,つまり V だけ小さくなると仮定しましょう.つまり,左の 10 円玉の,地面にたいする速さが,衝突後に v − V になるとします.
その場合について,右の 10 円玉から見た,左の 10 円玉の相対速度を考えましょう.衝突前に,右の 10 円玉から見て,左の 10 円玉は速さ v で近づきます.一方,衝突後の二枚の速さの差は,
V − ( v − V )
です.つまり,右の 10 円玉から見ると,左の 10 円玉は V − ( v − V ) の速さで遠ざかります.
さきに見た,ボールが壁ではねかえる例で,壁のところで見ているひとにとって,ボールは,速さ v で近づいて,衝突後に速さ v で遠ざかりました.それと同じように,右の 10 円玉から見て,左の 10 円玉は衝突後に速さ v で遠ざかると仮定しましょう.このとき,
| V − ( v − V ) | = | v | |
| V − v + V | = | v | |
| 2V | = | 2v | |
| V | = | v. |
つまり,衝突後の,右の 10 円玉の速さ V は v に等しく,左の 10 円玉の速さ v − V は 0 であるという結論が得られます.止まっている 10 円玉に別の 10 円玉が速さ v でぶつかると,止まっていた 10 円玉が速さ v で動きだし,はじめに動いていた 10 円玉が止まるという現象が,なんとか説明されました.
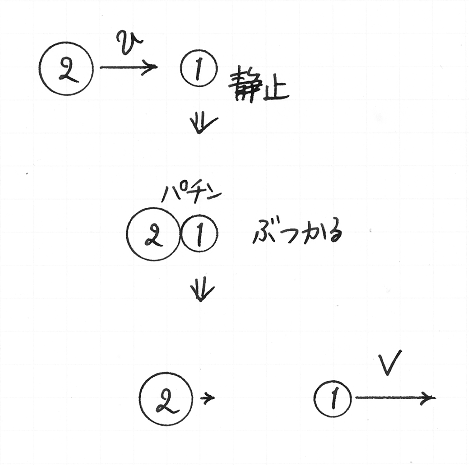 図 1-5-3 |
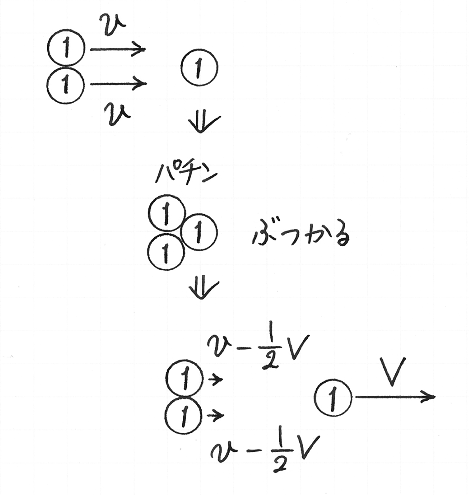 図 1-5-4 |
こんどは,重さが異なる二枚の硬貨が衝突する例について考えましょう.計算を簡単にするために,重さ 2 の硬貨が重さ 1 の硬貨にぶつかるとします.ふたつの硬貨の重さの比が,2 : 1 です.
重さ 2 の硬貨が,地面にたいする速さ v で動いていて,地面にたいして静止している,重さ 1 の硬貨にぶつかるとします.その衝突をきっかけにして,重さ 1 の硬貨が,地面にたいする速さ V で動きだし,重さ 2 の硬貨は減速するとします.
重さ 2 の硬貨がどれくらい減速するか,わたしたちには分かりませんが,さきに見た,物質の分割の考えに沿って,次のように仮定しましょう:重さ 2 の硬貨を,二個の重さ 1 の物体が結合したものと見なします;ふたつの硬貨がぶつかった「衝撃(impulse)」によって,重さ 1 の硬貨が速さ V で動きだします;その「衝撃」の「反動(reaction)」が,重さ 2 の硬貨のふたつの部分に均等に分かれて及んだとわたしたちは見なして,それらのふたつの部分がいずれも だけ減速すると仮定します;つまり,重さ 2 の硬貨の速さが,衝突後に になるとします.
そのとき,衝突後の二枚の速さの差は,
であり,重さ 1 の硬貨から見ると,重さ 2 の硬貨は速さで遠ざかります.ボールが壁ではねかえる場合や二枚の硬貨が衝突する場合と同じように,一方の側から見て,他方が近づいてくる速さと遠ざかる速さとが等しいと仮定しましょう.
| = | |||
| = | |||
| = | |||
| = | . |
つまり,衝突後の重さ 1 の硬貨の速さ V は で,衝突後の重さ 2 の硬貨の速さは,
| = | |||
| = | |||
| = | . |
重さ 2 の硬貨が速さ v で,静止している重さ 1 の硬貨にぶつかると,重さ 1 の硬貨が速さ で動きだし,重さ 2 の硬貨は速さ に減速しつつも動きつづけます.重い硬貨が軽い硬貨にぶつかると,軽い硬貨が動きだし,重い硬貨も減速しつつ動きつづけるという現象が,なんとか説明されました.
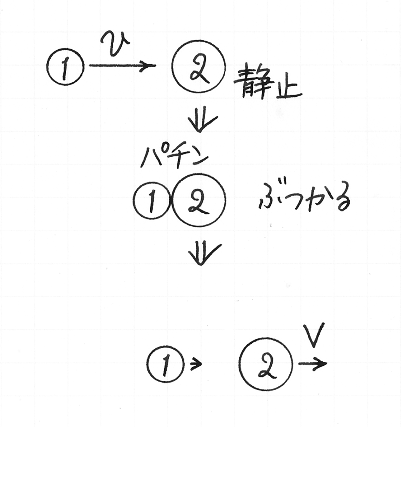 図 1-5-5 | 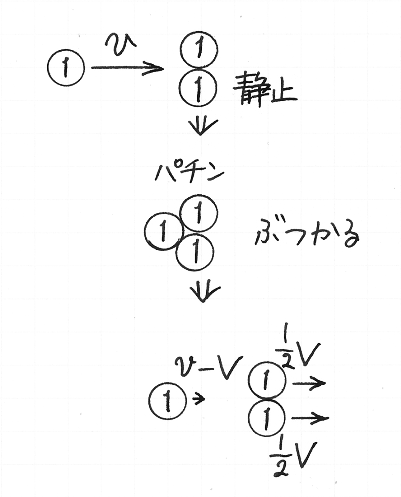 図 1-5-6 |
もうひとつ,重さ 1 の硬貨が重さ 2 の硬貨にぶつかる例を見ましょう.
重さ 1 の硬貨が,地面にたいする速さ v で動いていて,地面にたいして静止している,重さ 2 の硬貨にぶつかるとします.重さ 2 の硬貨をふたつの部分に分割して,その現象について考察しましょう.
二枚の硬貨がぶつかった「衝撃」によって,重さ 1 の硬貨が V だけ減速するとします.それと同じ大きさの「衝撃」が重さ 2 の硬貨のふたつの部分に均等に与えられるとすると,それぞれの部分が得る「衝撃」の大きさは,重さ 1 の硬貨が受けた「衝撃」の大きさの半分です.そこで,二枚の硬貨がぶつかったあと,重さ 2 の硬貨は速さ で動きだすと仮定します.つまり,衝突後の重さ 1,重さ 2 の硬貨の,地面にたいする速さが,それぞれ v − V, であるとします.
そのとき,衝突後の二枚の速さの差は,
であり,重さ 2 の硬貨から見ると,重さ 1 の硬貨は速さ で遠ざかります.これまでの場合と同じように,その速さが,衝突前に近づく速さ v に等しいと仮定すると,
| = | |||
| = | |||
| = | |||
| = | . |
つまり,衝突後の重さ 2 の硬貨の速さ は,
| = | |||
| = |
であり,重さ 1 の硬貨の速さ v − V は,
| = | |||
| = |
です.重さ 1 の硬貨が速さ v で,静止している重さ 2 の硬貨にぶつかると,重さ 2 の硬貨は速さ で動きだします.一方,重さ 1 の硬貨の衝突後の速さは という負の値で表されています.このことは,重さ 1 の硬貨が,もと来たほうへ速さ で進むことを意味していると,わたしたちは理解しましょう.軽い硬貨が重い硬貨にぶつかると,重い硬貨が動きだし,軽い硬貨がはねかえるという現象が,なんとか説明されました.
わたしたちは,先を急ぎません.物理に詳しいかたのなかには,いまわたしたちが見た衝突の例が「弾性衝突」にかぎられていることに不満をお持ちのかたがいるかもしれません.また,「衝撃(impulse)」,「反動(reaction)」と西欧語を併記してある語は,物理ではそれぞれ「力積(impulse)」,「反作用(reaction)」というのではないかといぶかしむかたもいるでしょう.いずれもそのとおりですが,みなさんが思っているところへ,わたしたちはあとで参ります.それより,わたしたちは,いま考察したことを一般化しましょう.
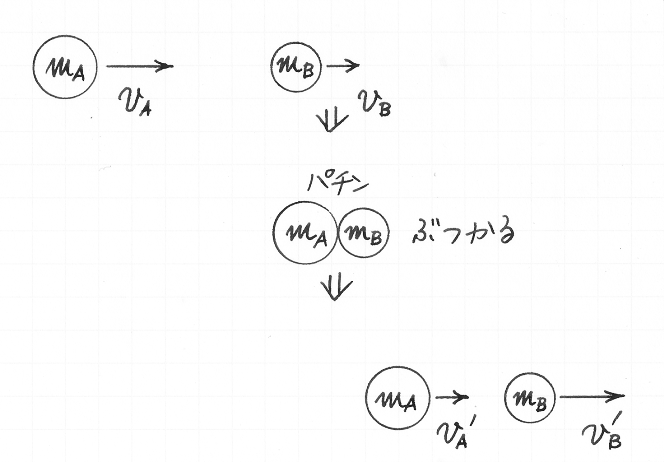 図 1-5-7 |
重さ mA,mB のふたつの物体が,それぞれ,地面にたいする速さ vA,vB (vA > vB)で,一直線上を同じほうに進んでいるとします.重さ mA の物体は,やがて重さ mB の物体に衝突します.重さ mA,mB の物体の,衝突後の地面にたいする速さを,それぞれ,vA',vB' とします.つまり,衝突によって,重さ mB の物体の速さは vB' − vB だけ増え,重さ mA の物体の速さは vA − vA' だけ減るとします.
ここで,重さ mA の物体は,重さ 1 の部分が mA 個だけ「集まったもの(mass)」であると,わたしたちは見なしましょう.重さ mB の物体は,mB 個の「集まり(mass)」です.ふたつの物体がぶつかった「衝撃(impulse)」が,重さ mA の物体の mA 個の部分に均等に分けあたえられ,重さ mB の物体の mB 個のあいだでも均等に分けられるとします.「衝撃(impulse)」の大きさを I とすると,重さ mA,mB の物体において,重さ 1 の各部分に分けあたえられる「衝撃(impulse)」の大きさは,それぞれ , ずつです.さきほどと同じように,これらの比が,
(mA の速さの減少分) : (mB 速さの増加分)
に等しいと仮定すると,
: = (vA − vA') : (vB' − vB).
外項の積と内項の積とは等しいので,
(vB' − vB) = (vA − vA').
両辺に をかけて,
mB (vB' − vB) = mA (vA − vA').
括弧を開いて,
mBvB' − mBvB = mAvA − mAvA'.
移項して,
mAvA' + mBvB' = mAvA + mBvB.
物理にお詳しいかたはお分かりのように,この方程式はのちに「運動量保存の法則」と呼ばれます.かりにわたしたちが,mA,mB,vA,vB の大きさを知っていて,vA',vB' の大きさを知らないとします.そのとき,もしわたしたちが,vA',vB' のすくなくとも一方を含む別の方程式を手に入れれば,その式と「運動量保存の法則」とを連立方程式と見なして,vA',vB' の大きさを求めることができます.二枚の硬貨がぶつかる例で,わたしたちは,「衝突前に硬貨 A から見て硬貨 B が近づいてくる速さ」と「衝突後に硬貨 A から見て硬貨 B が遠ざかる速さ」とが等しいと仮定して,vA',vB' の大きさを求めました.それらふたつの速さが等しいのは特殊な場合においてにかぎられることを,わたしたちはあとで見ますが,そのことと関係なく「運動量保存の法則」は成立します.ただし,上で得られた方程式で,mA,mB は「重さ」または「重さ 1 の部分の個数」を意味していて,物理の教科書に載っている「質量(mass)」ではありません.「質量」を用いた運動量保存の法則について,わたしたちはのちに見ます.
硬貨の衝突で見られる現象がある程度説明できたので,わたしたちは,その説明を先に進められるかどうか検討しましょう.二枚の硬貨が衝突すると,どちらの硬貨の速さも増えたり減ったりしました.同じように,硬貨にかぎらず,ふたつの物体が衝突するならば,それぞれの速さが増減する.そのことをわたしたちが疑う必要はないでしょう.
では,その逆は真でしょうか.つまり,物体の速さが変わったならば,その物体は他の物体と衝突したのでしょうか.そうでないことは明らかです.机のうえにある硬貨を指で弾くと,それは,他の物体と衝突しなくても,だんだん遅くなってやがて静止します.机と硬貨とのあいだに摩擦があるからです.ふたつの物体のあいだに摩擦があるのは,それらが接触しているからです.そこで,「衝突」を広い意味で「接触」の一種であると解釈して,こう言いかえましょう.物体の速さが変わったならば,その物体は他の物体と接触したのでしょうか,と.
かりに,それが真であると仮定しましょう.では,速さが変わらない運動とは,どんなものでしょうか.ルネ・デカルトが想定したのは,物体が宇宙空間をまっすぐに等速で進みつづけるような運動でした.その一方で,彼は地動説の正しさを確信していたので,その想定と地動説とを両立させようとしました.太陽のまわりを回る地球は,宇宙空間をまっすぐに進んでいるわけではありません.いま,わたしたちの仮定によれば,地球は,宇宙空間で他の物体と接触しているはずです.そこでデカルトは,宇宙空間に,人間の目に見えない渦があるという仮説を立てました.その渦が地球にぶつかることによって,地球は太陽のまわりを回っていると,彼は主張しました.もしその渦がなかったとすると,地球は,宇宙空間をまっすぐに等速で進み,その結果,太陽から遠ざかることだろう,と.
ところで,物体が,他の物体と接触することなく,その速さが変わらない運動は,なぜまっすぐでなければならないのでしょうか.言いかえれば,まっすぐでなく,たとえば円に沿って一定の速さで運動している物体は,他の物体と接触しているのでしょうか.
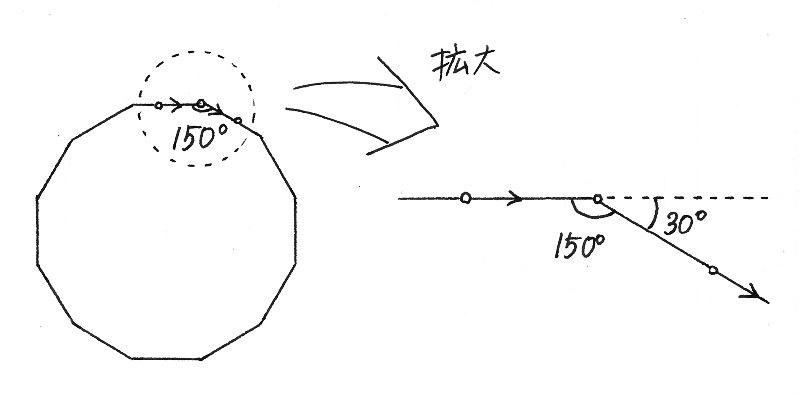 図 1-6-1 |
円を,正多角形の極限であると考えましょう.そして,円に沿った運動について考察する準備として,たとえば正十二角形に沿った運動について考えましょう.正十二角形のひとつの内角は 150º ()です.正十二角形の辺に沿ってまっすぎに進んできた物体の進行方向が,頂点で 30º ()だけ変わるとき,なにが起きているかを考えます.
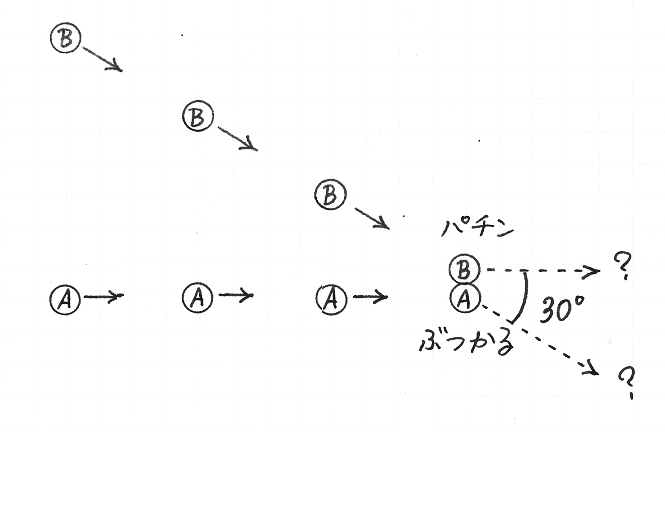 図 1-6-2 | 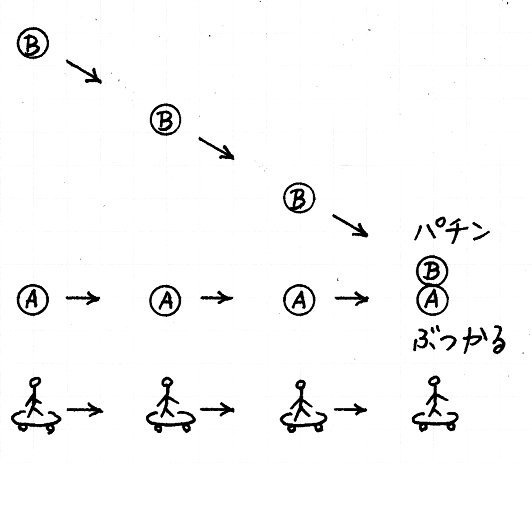 図 1-6-3 | 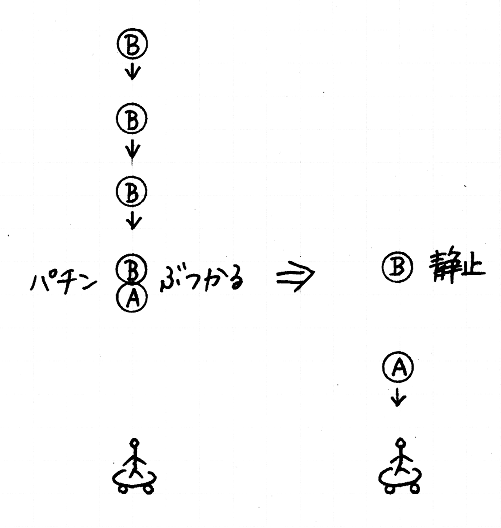 図 1-6-4 |
重さが等しいふたつの物体が,図 1-6-2 のように運動していて,やがて衝突するとします.衝突後のそれぞれの物体の運動は,どのようなものでしょうか.図 1-6-3 のように,物体 A と同じ方向に同じ速さで運動している観測者が見れば,A は静止していて,B が A に近づいています(図 1-6-4).さきに「重さが等しい二枚の硬貨の衝突」の事例でわたしたちが見たように,物体 A,B の重さが等しいならば,衝突後,B は静止し,A は,衝突前の B の速さと等しい速さで動きだします(図 1-6-4).その現象をもとの視点で見ると,衝突後の A は,衝突前の B が進んでいた方向と平行に進みます(図 1-6-5).言いかえれば,A の進行方向が 30º だけ変わります.
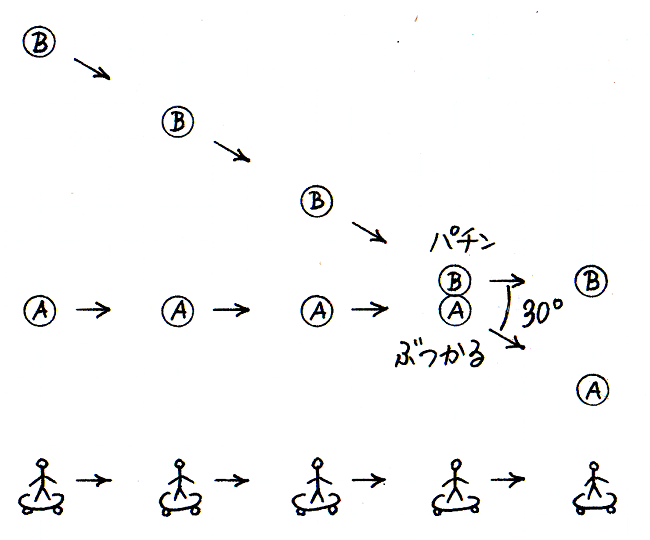 図 1-6-5 | 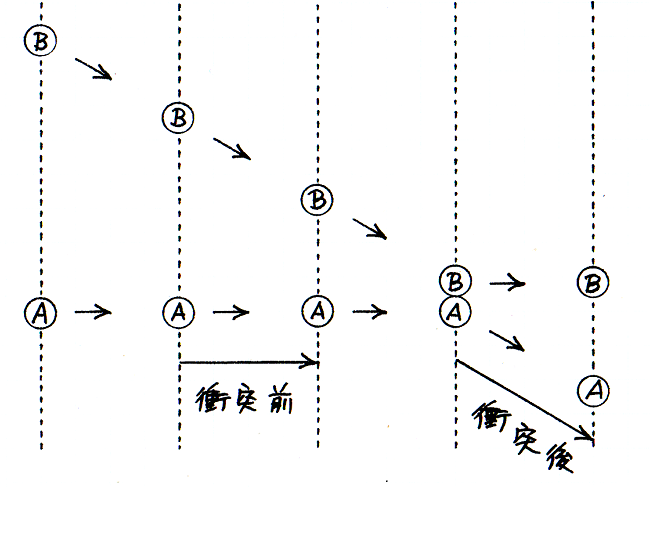 図 1-6-6 |
ただし,この例では,A の衝突前の速さと衝突後の速さとが等しくありません.衝突後の A は,図 1-6-6 のように斜めに進むので,単位時間(たとえば 1 秒間)に進む道のりが衝突前より長くなっています.衝突の前後で A の速さが変わらないようにするには,衝突前に A と同じ方向に同じ速さで進んでいる観測者から見て,B が A に斜めから衝突しなければなりません.
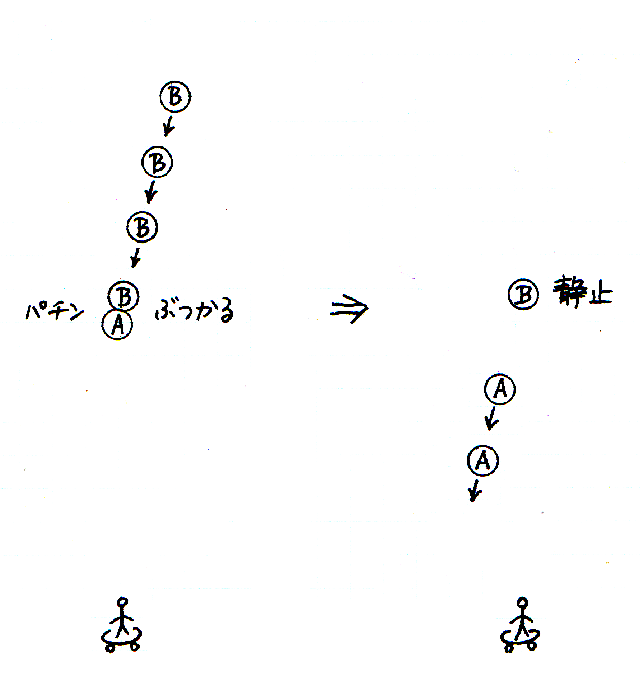 図 1-6-7 | 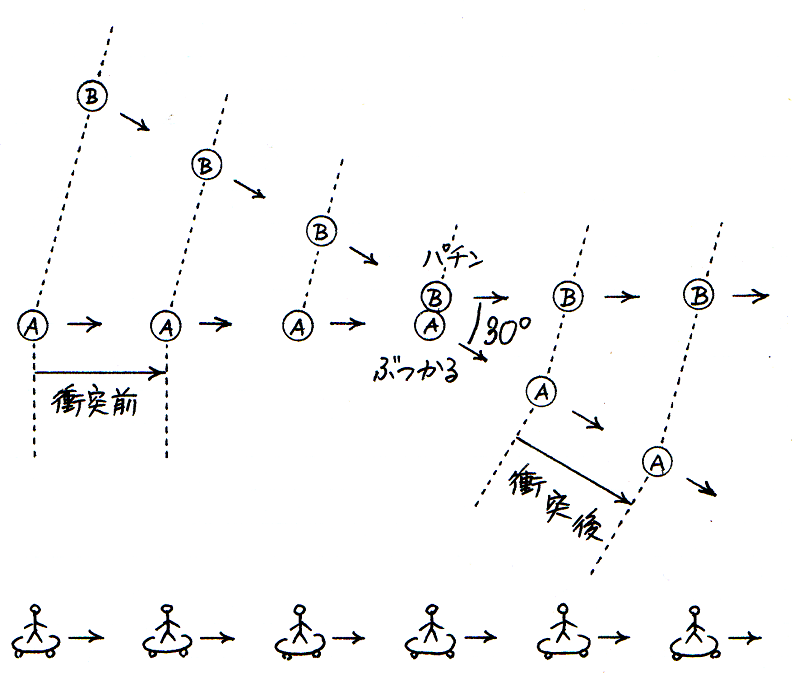 図 1-6-8 |
正十二角形にたいして静止している視点から,その運動は,図 1-6-8 のように見えます.衝突前の B の方向と速さとをうまく設定すれば,わたしたちは,A が進む方向を 30º だけ変え,かつ,衝突の前後で A の速さを変えないことができます.
ふたつの物体が衝突すると,一方の物体の速さが変化しないけれども,それが進む方向が変化する場合があると,この例は示しています.論理学で,逆はかならずしも真でありません.「物体の速さが変わらないものの,それが進む方向が変わるならば,それは他の物体と衝突している」が真であるかどうかを,わたしたちは論理で決めることができません.しかし,わたしたちは,上の例を見たので,物体が他の物体と衝突しなくても上の例と同じ現象が起こると考えづらくなりました.そこで,物体が一定の速さで進みつつ,その方向を変えるとき,それは他の物体と衝突していると,わたしたちはしばらく考えることにします.
 図 1-6-9 |  図 1-6-10 |
地球が円に沿って太陽のまわりを公転する運動について考察するのであれば,わたしたちは,正十二角形より頂点が多い正多角形の辺に沿った運動を考えたのちに,その頂点を増やしてその極限を考えなければなりません.さきほどの考察で,正十二角形の辺に沿って運動する物体 A と,それに衝突する物体 B とは,重さが等しいとわたしたちは前提していました.その場合,正十二角形に沿って一定の速さで運動する物体は,各頂点で,外から来る別の物体と 図 1-6-9 のように,衝突します.正多角形の頂点が増えるにつれて,頂点で衝突する物体が増える一方,一度の衝突ごとに変わる進行方向の角は小さくなります.図 1-6-10 は,そのようすを表しています.宇宙空間に渦があると主張したデカルトの気持ちが察せられます.
しかし,地球に衝突する物体が,地球と同じ重さをもってなければならない理由はありません.地球に衝突する物体は,人間の目に見えないので,とても小さくて軽いかもしれません.重い物体が与えたのと同量の「衝撃(impulse)」を軽い物体が地球に与えるためには,軽い物体は地球に速く衝突しなければなりません.
たとえば,正十二角形の一辺に沿って運動している物体 A があって,それと同じ方向に同じ速さで進んでいる観測者がいるとします.その観測者から見て辺に垂直な方向から近づいてきた軽い物体が,物体 A に衝突するとします.そのようすは,観測者にとって,図 1-6-11 のように見えます.
その現象は,正十二角形にたいして静止している視点から,図 1-6-12 のように見えます.その視点で見ると,軽い物体の方向は,辺に垂直でありません.
 図 1-6-12 |  図 1-6-13 |
さきほどの例と同じように,この例でも,衝突後に A が斜めに進むぶん,衝突前よりすこし速くなります.それを補正するために軽い物体の方向を調整すると,正十二角形にたいして静止している視点から見て,衝突前の A と軽い物体との方向がなす角は,90º ()に近づきます.きわめて軽い粒子ならば,地球に十分な「衝撃(impulse)」を与えるために,きわめて速く地球に衝突することでしょう.その場合にも,正十二角形にたいして静止している視点から見て,衝突前の両者がなす角は,90º ()に近づきます.
図 1-6-14 は,きわめて軽い粒子がきわめて速く地球に衝突することによって,地球が太陽のまわりを公転しているようすを示しています.古代ギリシャ哲学に詳しいかたは,この図を見て,原子がそれ自身の重さによって落下するという,エピクロスの原子論を思いだすかもしれません.物理に詳しいかたには,この図が,アイザック・ニュートンの重力理論に符合していると映るかもしれません.この図のような衝突を仮定すると,重力が逆二乗力であることを説明できそうだからです.中心を共有する大小ふたつの球があるとして,それらの半径の比を 2 : 1 としましょう.球の中心のほうへまっすぐに進む多数の軽い粒子が,大きいほうの球面の一部の領域を通過したあと,そのまま小さい球面を通過するとします.大きい球面の領域の面積を S とすると,その領域を通過した粒子が小さい球面上で通過する領域の面積は S です.つまり,小さい球面を通過する単位面積(たとえば 1 m2)あたりの粒子の個数は,大きい球面の単位面積あたりの個数の 4 倍です.距離が 倍(k は正の実数)になると,大きさが k2 倍になる力を逆二乗力といい,ニュートンが提唱した万有引力はその代表例のひとつです.
 図 1-6-15 |  図 1-6-16 |
しかし,万有引力の法則は,惑星にはたらく引力の大きさが,距離の逆二乗に比例することに加えて,惑星の「質量 (mass)」に比例すると主張しています.わたしたちがここまで見てきた衝突(および接触)の理論は,「質量 (mass)」の概念に基づいていません.わたしたちが見てきた,運動量についての素朴な理論は,ニュートンによって,「質量 (mass)」の概念を用いて全面的に改められます.わたしたちは,そろそろ「質量 (mass)」について考察しなければなりません.
アイザック・ニュートンは,原子について独特の洞察をもっていたと思われます.端的に言えば,原子の種類はひとつだけであると彼は考えていたと思われます.各々の原子は,それがいつどこにあるという点でその他の原子と区別されるものの,大きさや性質の点で,どの原子も他の原子と区別がつかない,と.その考えは,今日わたしたちが学ぶ化学の見解と異なっています.
わたしたちはここで,元素や原子についておさらいをしておくほうがいいかもしれません.古代から近代化学の黎明期に至るまでの長い年月のあいだ,元素の定義は単純でした.「この世界のものは究極的になにでできているか」という問いへの答えになるものが,元素でした.古代ギリシャでは,土,水,風,火が元素であると考えられたことがありました.水素と酸素とが化合して水が生じる現象が 18 世紀に発見されると,水に替わって,水素や酸素が元素であると見なされました.それらが,別の物質に分解されなかったからです.
一方,原子論はもともと,なにが元素であるかという問いに関係がありません.たとえば,鉄板をふたつに切断して得られる欠片は,どちらも鉄でできています.そのかけらを切断し,そうして得られた欠片をさらに切断することを繰りかえすと,各々の欠片は,やがて,それ以上分けることができない最小の単位に至るか,それとも,かぎりなく切断を繰りかえしても欠片は鉄でありつづけるか.古代から近代化学の黎明期に至る長い年月のあいだ,原子論の定義は単純でした.その問いにたいして,欠片はやがて最小の単位に至るという主張が,原子論と呼ばれました.
今日わたしたちが学習する化学で,元素や原子の定義は,それほど単純でありません.原子は内部構造をもち,どの原子も,陽子や中性子,電子などから成ることが 20 世紀に発見されたからです.もしそのとき化学者たちが,「元素」という語を古代以来の意味で使いつづけようとしたならば,彼らは,陽子や中性子,電子を「元素」と呼んでいたことでしょう.そのときの最新の知見で,「この世界のものは究極的になにでできているか」の答えに,それらがなったからです.また,同時に,陽子や中性子,電子が「原子」と呼ばれていたことでしょう.しかしそのころには,科学者たちや化学に関連している人々の集団が大きくなりすぎて,つい昨日まで元素や原子と呼ばれていたものを,翌日から別の名で呼ぶことが困難になっていました.「元素」や「原子」の名で,昨日までと別のものを呼ぶことも.その結果,「原子 (atom)」は,ギリシャ語の「分けられないもの」という原義に反して,ひとつの原子核とそのまわりのいくつかの電子とから成ると説明されることになりました.そして,化学者たちは,原子核を構成する陽子,中性子のうち,陽子の個数によって原子を分類し,陽子の個数が等しい原子の集合ごとにひとつずつ元素の名を付けることにしました.
ニュートンは,のちの時代の化学者たちの見解におかまいなく,原子は一種類しかないという独自の洞察をもっていたと思われます.今日の化学の教科書で言われている意味で「原子」という語を理解するならば,ニュートンは誤っていたと見なされます.しかし,その語を原義の「分けられないもの(atom)」と理解するならば,それは,陽子や中性子,電子を指しているかもしれませんし,クォークを指しているかもしれませんし,さらに超弦などの今後発見されるかもしれない実体(substance)を指しているかもしれません.原子が一種類しかないという洞察は,今日多くの物理学者が胸中もっている洞察とかけ離れているわけでありません.
わたしたちはここまで,そういった洞察をニュートンがもっていたと思われると言うにとどめて,断定をしていません.彼は,著作のなかで原子について論じていますが,原子が一種類であると考えていると明確に記していないからです.ガリレオ・ガリレイやルネ・デカルトが,地動説に確信をもちつつ,迫害を恐れてそれを気軽に主張できなかったように,ニュートンも,自分の社会的な立場を脅かしかねない信仰をもっていました.彼は,ユニテリアンでした.原子についての彼の考えとユニテリアニズムとは直接の関係がありませんが,彼は用心深かったので,望まない論争で本音を言わざるをえなくなることを懼れて,彼の原子論を発表しなかったのかもしれません.わたしたちは,状況証拠から,彼の考えを理解しようとしています.
ニュートンは,『自然哲学の数学的諸原理』(1687)で,質量を次のように定義しています:
物質の量(羅 quantitas materiæ,英 quantity of matter)とは,物質の密度と大きさ(体積)とをかけて得られる,物質の測度である.『自然哲学の数学的諸原理』定義,定義 I
ニュートンはその定義のあと,次のように付けくわえます:
このあと,わたくしが,物体(羅 corporis,英 body)または質量(羅 massa,英 mass)の名で意味するものは,どこにおいても,この量である.この量は,それぞれの物体の重さとしても知られている.というのは,それは重さに比例するからである.そのことを,わたくしは,とても精密に作られた振子の実験によって見出したので,のちに示すことになるだろう.
今日のわたしたちにとって,この定義は奇妙です.わたしたちは,密度を「単位体積(たとえば 1 m3)あたりの質量」であると理解しています.「質量」を定義するまえに,密度(単位体積あたりの質量)を定義することなど,わたしたちにはできません.ニュートンの言う「密度」の意味は,わたしたちが知っているものでないようです.
ここで,あらゆる物体は一種類の<原子>(それは陽子でも中性子でもクォークでも未発見の実体でもかまいません)から成ると仮定しましょう.すると,あまたある物質のあいだの性質の違いは,どのように説明されるでしょうか.あらゆる物質の素材が,どんな物質にも共通の,一種類の<原子>であるならば,それぞれの物質の性質は,たとえば,<原子>が形成する構造によって決まるかもしれません.複数の<原子>が集まって,線を成すか,面を成すか,四面体や六面体などの立体を成すか,さらにそれらがどのような二次構造,三次構造などの高次構造を成すか,そういった構造によって,それぞれの物質の性質が決まるかもしれません.もしかすると,構造以外に物質の性質を決める原因があるかもしれません.たとえば,<原子>が一定数以上集まると,それ以前に個々の<原子>がもっていなかった性質を集合体がもつと仮定したり,運動している<原子>は,静止しているときにない性質をもつと仮定したりすることによって,あまたある物質の性質の違いを説明できるかもしれません.しかし,いまのところ必然性のないそういった仮定を置くより,まず構造の違いに注目するほうが合理的です.
どんな物質も,すべての物質に共通する一種類の<原子>の「集まり(mass)」であり,各々の物質の性質は<原子>が形成する構造によって定まると仮定します.そのとき,鉄や硫黄といったそれぞれの物質は,その独自の構造をもっていますから,単位体積(たとえば 1 m3)あたりに含まれる<原子>の個数は物質ごとに定まっていると考えられます.そこで,単位体積あたりに含まれる<原子>の個数に比例するなんらかの量を定義して,それを「密度」と呼べば,「密度」はそれぞれの物質ごとに定まっていると考えられます.ニュートンの念頭にあった「密度」がそういったものであるならば,彼による「質量(mass)」の定義で,なぜ「密度」が「質量」に先立つ所与の量として扱われているか,わたしたちは理解できます.
いまわたしたちは,「密度」を,単位体積あたりに含まれる<原子>の個数に比例する量と言いました.しかし,比例する量でなく,単位体積あたりの<原子>の個数そのものを,「密度」と言っていけない理由はありません.いまの段階で,そう言わないふたつの理由があります.ひとつは,<原子>の大きさが分からないので,<原子>を数える方法がないこと.もうひとつは,たとえ<原子>を数える方法が見つかったとしても,その個数は膨大でしょうから,ある程度の量をひとまとめにして,煩わしさを避けるほうが利口であるということです.
しかし,そのどちらの理由も本質的でありませんから,わたしたちはここで試しに,「密度」を,「単位体積あたりに含まれる<原子>の個数」と定義します.その定義に基づいて,ニュートンによる「質量」の定義をふたたび見ましょう:
| (質量) | = | (密度) × (体積) | |||
| = | ( | 単位体積あたりに 含まれる原子の個数 |
) | × (体積) | |
| = | (原子の個数). | ||||
このように,物体の質量とは,その物体を構成する<原子>の個数であるようです.たとえ,「密度」を,「単位体積あたりに含まれる<原子>の個数に比例する量」と定義したとしても,物体の質量とは,その物体を構成する<原子>の個数に比例する量です.わたしたちの目に見えないほど小さい<原子>が何個集まって物体を構成しているかということは,わたしたちの目に見える運動に,なにかの関係があるでしょうか.わたしたちは,どんな現象を考察するさいに,「質量(mass)」を必要とするでしょうか.その答えを目指すまえに,わたしたちは道草をして,等速直線運動について見ておきましょう.
物体の運動を変える原因について論じるには,まず,変化しない運動を定義する必要があります.それが,等速直線運動(uniform motion)です.物体の運動を変える原因は,他の物体との衝突あるいは接触であると,ルネ・デカルトは考えました.さきにわたしたちが見たように,円周に沿って一定の速さで運動している物体は,たえず他のいくつもの物体と衝突している可能性があります.つまり,たとえ物体が他の物体と衝突しても,物体の速さが変わらず,運動の方向だけが変わることがあります.そこでデカルトは,速さも方向も変わらない運動を,一様な運動(uniform motion)と見なしました.
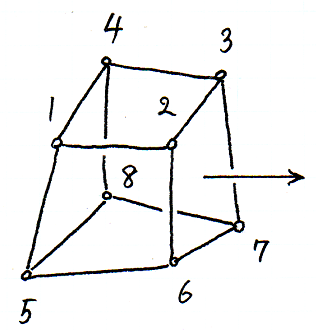 図 1-8-1 |
さて,図 1-8-1 のように,8 個の<原子>(ニュートンの意味での原子)から成る物体があって,それが運動しているとします.その図では,どの<原子>も,近くにある 3 個の<原子>と糸のようなもので結びついていると示されていますが,もしそのような糸が実在するのであれば,その糸もまた<原子>から成るものでなければなりません.すると,その物体は,8 個の<原子>から成ると言えません.そこで,それらの糸は,8 個の<原子>がひとつのかたまり(mass)であることを示す,想像上のものであると,わたしたちは見なすことにします.
8 個の<原子>のひとつずつに,1,2,…,8 の番号を振り,それぞれの速さを v1,v2,…,v8 とします.簡単のために,8 個の<原子>は平行に運動しているとします.速さ v1,v2,…,v8 のなかに,ひとつでも他と異なるものがあるならば,物体の形は変化しつつあります.そのとき,わたしたちは,物体全体の速さをどのように定義すればいいでしょうか.物体の部分によって速さが異なりますから,8 個の<原子>の速さの平均値を,物体全体の速さ v と,わたしたちは定義しましょう.
.
 図 1-8-2 |
この例で,8 個の<原子>が集まっていることに特別な意味はありません.次に,m 個の<原子>から成る物体が運動しているとします.上の例と同じように,m 個の<原子>は平行に運動しているとし,<原子>のひとつずつに,1,2,…,m の番号を振り,それぞれの速さを v1,v2,…,vm とします.そして,m 個の<原子>の速さの平均値を,物体全体の速さ v と定義しましょう.
.
ところで,v1,v2,…,vm のそれぞれの値は,他の値と異なるかもしれないので,場合によって,やがていくつかの<原子>どうしが衝突するかもしれません.もし<原子>どうしが衝突したら,それらの速さは,衝突前の速さから変化するでしょうし,物体全体の形は変化するでしょう.しかしそのことは,m 個の<原子>から成る物体の内部で生じる現象です.たとえ内部の<原子>どうしが衝突しても,m 個の<原子>から成るひとかたまりの物体が,他の物体と衝突あるいは接触しないかぎり,その運動は変化しません.内部の<原子>どうしが衝突したあとの 1,2,…,m の<原子>の速さを,それぞれ v1',v2',…,vm' とすると,さきほどと同じ v を用いて,次の式が得られます.
.
m は,<原子>の個数を表す定数ですから,物体が他の物体と衝突あるいは接触しないかぎり,積 mv は一定です.
 図 1-8-3 |
つづいて,(mA + mB) 個の<原子>から成る物体があって,それが運動しているとします.この場合も,簡単のために,すべての<原子>は平行に運動しているものとします.
ここで,図 1-8-3 のように,物体のなかに<原子>が存在しない部分があるとしましょう.原子が存在しない空間を物体の一部と見なしていいかどうか悩ましいかもしれませんが,わたしたちは,8 個の<原子>から,そして,m 個の<原子>から成る物体について考察したとき,<原子>と<原子>とのあいだに隙間があると考えました.ですから今回も同じように,物体にすこし大きめの隙間があると考えることにしましょう.
この物体を成す (mA + mB) 個の<原子>のうち,mA 個は隙間の左方にあり,残りの mB 個は隙間の右方にあるとします.mA 個から成る部分の原子のひとつずつに 1,2,…,mA の番号を振り,残りの mB 個から成る部分の原子のひとつずつに mA + 1,mA + 2,…,mA + mB の番号を振って,<原子>の速さをそれぞれ v1,v2,…,vmA,vmA + 1,vmA + 2,…,vmA + mB とします.そして,(mA + mB) 個の<原子>の速さの平均値を,物体全体の速さ v とします.
.
さらに,隙間の左方にある mA 個の<原子>の速さの平均値を vA,右方の mB 個の速さの平均値を vB とします.ここで簡単のために,v,vA,vB はいずれも図の右に向いているとします(もしv,vA,vB や v1,v2,…,vmA + mB のなかに左向きのものがあるならば,それは負の値をとると見なすと,ここでの議論が成立します).
それぞれの式の両辺に mA,mB をかけて,
さきに得た に,これらの式を代入して,
.
ここで,vA > vB であるとすると,mA 個の<原子>から成る部分は,mB 個の<原子>から成る部分にやがて衝突するでしょう.その結果,それぞれの部分の速さが,vA',vB' に変化するとします.
そのとき,1,2,…,mA,mA + 1,mA + 2,…,mA + mB の<原子>の速さがそれぞれ v1',v2',…,vmA',vmA + 1',vmA + 2',…,vmA + mB' であるとすると,
これらふたつの部分の衝突は,(mA + mB) 個の<原子>から成る物体の内部で生じる現象です.たとえ内部の<原子>どうしが衝突しても,(mA + mB) 個の<原子>から成るひとかたまりの物体が他の物体と衝突あるいは接触しないかぎり,その運動は変化しません.言いかえれば,v は一定です.
.
さきほどの式の両辺に,それぞれ mA,mB をかけると,
が得られますから,これらを上の式に代入して,
.
この式と,さきほどの とより,
という方程式が得られます.もし結論を急ぐならば,この方程式が,教科書に載っている運動量保存の法則ですが,わたしたちは,ここでもまたゆっくりと進みましょう.
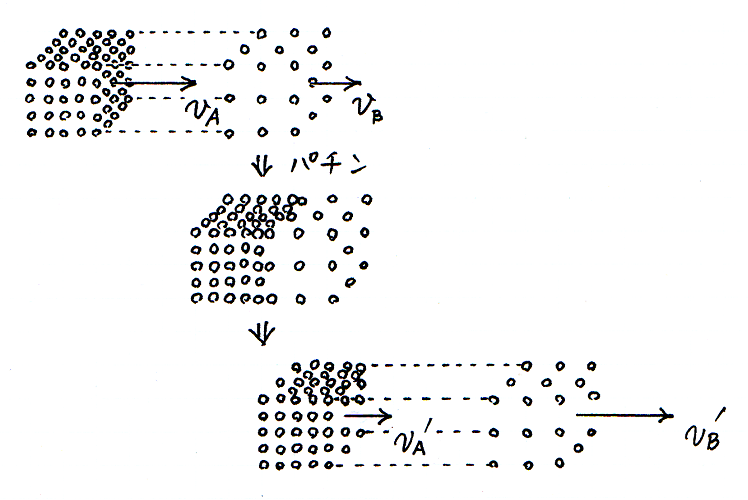 図 1-8-4 |
いま,わたしたちは,(mA + mB) 個の<原子>のかたまり(mass)をひとつの物体と見なし,mA 個の<原子>から成る部分,mB 個の<原子>から成る部分をいずれも全体の一部であると見なしてきました.しかし,わたしたちはここで見かたを変えて,mA 個,mB 個の<原子>から成るふたつのかたまりを,別の物体であると見なしましょう.わたしたちはこれまでも,ひとつの物体をいくつかの部分に分けて考えてきました.そのとき,わたしたちは,各部分がたがいに等しいように物体を分けました.しかしここでは,(mA + mB) 個の<原子>から成る物体を,mA 個,mB 個の<原子>から成る,ふたつの等しくない物体に分けて考えようとしています.それらふたつのかたまり(masses)を別の物体と見なすとき,わたしたちが当初ひとつの物体と見なしていた (mA + mB) 個の<原子>全体を,系(system)といいます.物体も系も,<原子>から成るかたまり(mass)であるという点で共通していて,ふたつのあいだに本質的な違いはありません.わたしたちが,なにをひとつと見なすかによって,呼びかたが変わるにすぎません.すると,さきほどわたしたちがふたつの部分の衝突と考えた現象は,ふたつの物体の衝突として,次のように記述されます.
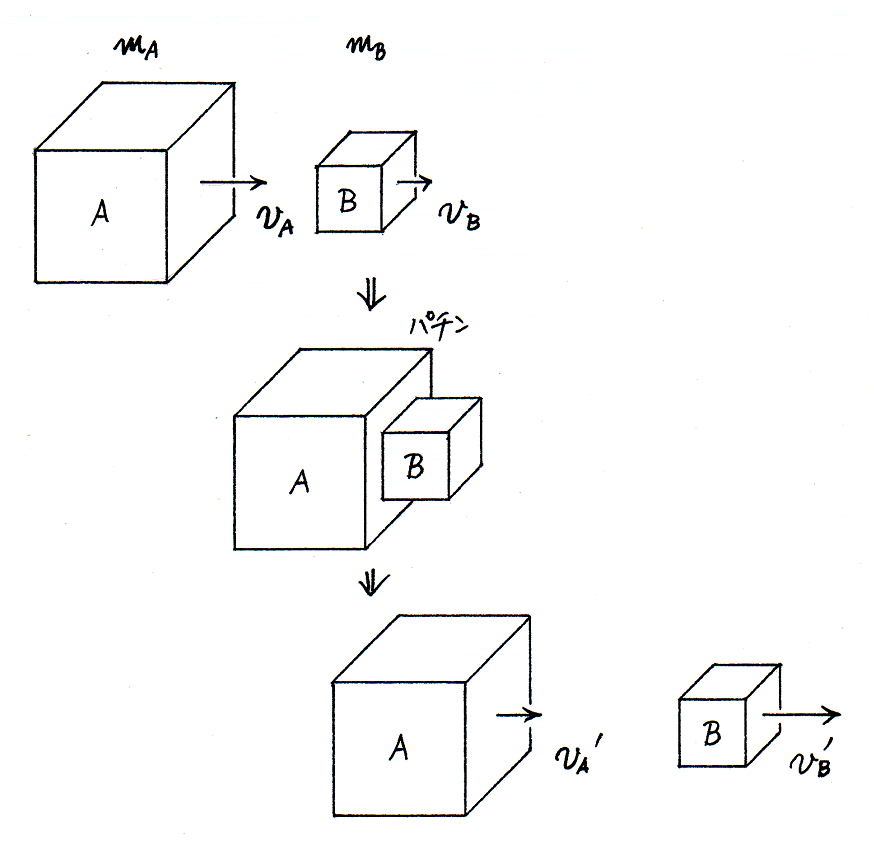 図 1-8-5 |
mA 個の<原子>から成る物体 A と mB 個の<原子>から成る物体 B とが,ひとつの直線に沿って,いずれも図 1-8-5 の右方に進んでいるとします.はじめ物体 A,B の速さがそれぞれ vA,vB であるとします.vA > vB とすると,物体 A はやがて B に衝突するでしょう.その結果,それぞれの速さが vA',vB' に変化するとします.
いまかりに,物体の<原子>の個数と速さとの積を運動量(momentum)と呼ぶことにすると,衝突前の物体 A,B の運動量はそれぞれ mAvA,mBvB であり,衝突後にそれらはそれぞれ mAvA',mBvB' という値をとります.わたしたちがさきほど行った考察によれば,ふたつの物体 A と B とから成る系が他の物体と衝突あるいは接触しないかぎり,
という方程式が成立します.明白な変化が起こっているにもかかわらず,その変化の前後でなにか不変のものがあるならば,それは「保存されている conserved」と表現されます.ここでは,ふたつの物体から成る系の運動量の和が保存されています.このことを,運動量保存の法則(the law of conservation of momentum)といいます.
ところで,わたしたちは以前,ふたつの物体が衝突するさいに,両者に同量で逆向きの「衝撃(impulse)」が与えられるという議論をしていたとき,上の法則と一見同等な意味をもっているかのような方程式を得て,すぐにそれを手放しました(1-5. 運動量の素朴な姿「素朴な運動量の一般化」).以前の方程式とこの方程式とは,たとえ見かけが同じであっても,成立する条件が異なるからです.以前の方程式で,mA,mB は,物体を成す<原子>の個数でなく,物体の重さを表しました.また,以前の方程式を導くさい,わたしたちは真偽不明の仮定を置いていました.それは,衝突するふたつの物体の一方に固定された観測者が見ると,もう一方の物体が速さ v で近づいてきて,衝突後に速さ v で遠ざかるというものでした.その仮定は,現実には,つねに成立するわけでありません.そして,その仮定が成立しない場合にその方程式が成立するかどうか,わたしたちは確かめていませんでした.一方,mA,mB を<原子>の個数と解釈してふたたび同じ方程式を導いたさい,わたしたちは,そのような仮定を置きませんでした.つまり,一方の物体から見て,他方の物体の速さが衝突の前後で変わらないような衝突でなくても,どんな衝突の前後でも運動量保存の法則が成立すると,わたしたちはここで初めて知りました.
近代科学において初めて運動量という概念を提唱したのは,ルネ・デカルトであるとしばしば見なされます.しかし,アイザック・ニュートンの観点に立つと,デカルトの言う運動量には修正が必要でした.デカルトは,『哲学原理』(1644)で次のように記しています:
動いている物体が他の物体に衝突するとき,もし動いている物体の,ひとつの直線に沿って動きつづける力が,もう一方の物体の抵抗より小さいならば,動いている物体の,方向は入れかわるが,運動は減らない.『哲学原理』二部四十節
この文は,わたしたちがさきに 1-5. 運動量の素朴な姿 で見た例のひとつを指していると読みとれます.デカルトは,速さ v で壁に衝突したボールが速さ v ではねかえる現象で,運動量が保存されると考えていました.
 図 1-5-1(再掲) |
もしデカルトの言うとおりに考えるならば,わたしたちは,この例でボールだけに注目して,衝突の前後で運動の量 mv は変化しないと見なさなければならないでしょう(わたしたちは,素朴な運動量について考えたとき,m を「重さ」としましたが,デカルト本人によれば,速さ v にかける係数 m は,物体の「大きさ」です).しかし,ニュートンの意味で運動量が保存されるのは,ボールが他の物体と衝突しないかぎりにおいてです.この例で,ボールは壁に衝突していますから,その運動量は保存されません.
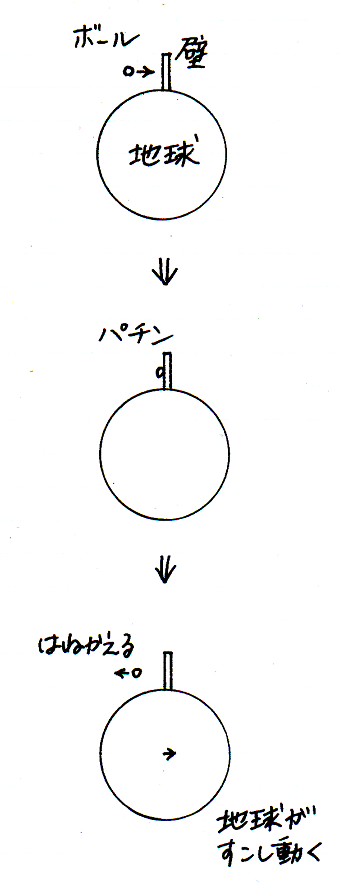 図 1-8-6 |
この例で保存されるのは,ボールと地球とから成る系の運動量です.ボールがぶつかった壁および地球は,衝突後,ボールがはねかえるのと逆のほうへわずかながら動きます.そのことによって,ボールと地球とから成る系の運動量は保存されます.
上の例でデカルトが陥ったような誤りを避けるには,速さに向きがあると考えることが,ひとつの有効な方法です.具体的に言うと,速さ(speed)に正負の符号を付けて,物体が動いている向きを区別することです.速さに正負の符号を付けて,どちら向きにどれだけの速さで動いているかを表せるようにした量を,速度(velocity)といいます.わたしたちは今後,「速さ」を「速度の大きさ(速度の絶対値)」と考えて,「速さ」と「速度」とを区別します.上の例で,ボールが壁に近づく速度を v とすると,はねかえって進むボールの速度は −v です.
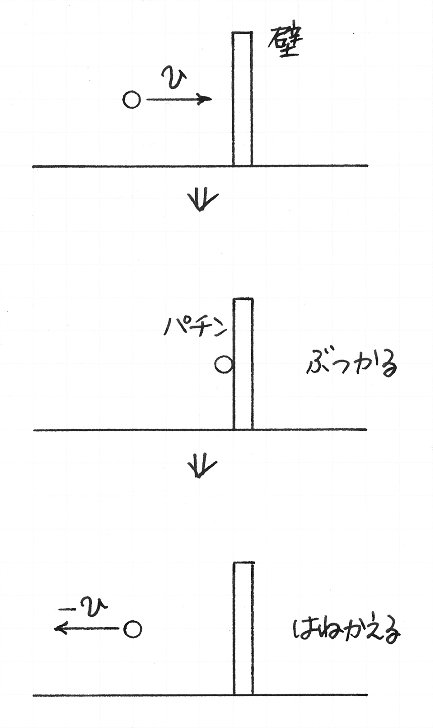 図 1-8-7 |
わたしたちはさきほど,かりに,物体の原子の個数と速さとの積を運動量と呼びましたが,今後は運動量を,原子の個数と速度との積としましょう.すると,上の例で,壁に近づいているときのボールの運動量は mv であり,はねかえって進むときの運動量は −mv です.両者は異なりますから,ボールの運動量は保存されていないと,わたしたちは容易に知ることができます.
ここで,わたしたちはいったん立ちどまって,1-7. 原子についてのニュートンの考え,1-8. 運動量保存の法則 で通ってきた道を振りかえりましょう.わたしたちは,どんな現象を記述するのに質量という概念が必要であるかという問いから出発しました.そのさい,わたしたちは,どんな物体も他の物体と共通の一種類の<原子>から成っていると仮定し,物体を成す<原子>の個数をその物体の質量と定義しました.次に,系の速度を,
| (系を成す<原子>の速度の和) | = (系の速度) | |
| (系を成す<原子>の個数) |
| (A を成す<原子>の速度の和) + (B を成す<原子>の速度の和) | = (系の速度) | |
| (A を成す<原子>の個数) + (B を成す<原子>の個数) |
| (A を成す<原子>の速度の和) | = (A の速度) | |
| (A を成す<原子>の個数) | ||
| (B を成す<原子>の速度の和) | = (B の速度) | |
| (B を成す<原子>の個数) |
| (A を成す<原子>の速度の和) = (A を成す<原子>の個数)·(A の速度) | |
| (B を成す<原子>の速度の和) = (B を成す<原子>の個数)·(B の速度) |
| (A を成す<原子>の個数)·(A の速度) + (B を成す<原子>の個数)·(B の速度) | = (系の速度) | |
| (A を成す<原子>の個数) + (B を成す<原子>の個数) |
| (A を成す<原子>の個数)·(A の速度) + (B を成す<原子>の個数)·(B の速度) |
| (物体 A を成す<原子>の個数)·(A の速度) + (物体 B を成す<原子>の個数)·(B の速度) |
| (物体 A を成す<原子>の個数)·(A の速度) |
以上の議論に,「原子の個数」は不可欠です.しかし,アイザック・ニュートンの時代に,原子が実在することは検証されていませんでした.そして,どんな物質にも共通する一種類の原子だけが存在するという洞察は,ニュートンが表沙汰にしたくない信仰,ユニテリアニズムとの関係を疑われるおそれがありました.そこで彼は,「原子の個数」を「質量(mass)」と言いかえ,まるで「密度」や「質量」が無定義語であるかのように
| (密度) × (体積) = (質量) |
なめらかな斜面を転がる球が進む道のりは,それが転がりはじめてからの「時間 time」の二乗に比例すると,ガリレオ・ガリレイは実験によって明らかにしました.つまり,時間が 1,2,3,⋯ と経つにつれて,球は 1,4,9,⋯ の道のりを進みます.その結論を得るまでに彼が行った工夫や苦労は,『新科学対話』(1638)に記されています.たとえば彼は,高いところに置いた水槽に管を付けて,その端を指で押さえ,時間を計りたいあいだだけ指を離して水が流れでるようにし,その水の重さを天秤で量って,その重さを「時間(time)」の代用物としました.
 図 2-1-1 |
球が転がりはじめてからの時間を t,進む道のりを x とすると,道のり x が時間 t に比例するので,
x = kt2 (k は比例定数)
という方程式が成立します.道のり x をメートルで,時間 t を秒で計るとすると,k は斜面の傾きのみによって決まる定数です.球が転がりはじめてから 1 秒後,2 秒後,3 秒後,⋯ までに進む道のりは,それぞれ k (m),4k (m),9k (m),⋯ です.
では,球が転がりはじめてからちょうど 1 秒後の,球の速さはいくらでしょう.速さは,
(速さ) = (道のり) ÷ (時間)
で求められますから,球が転がりはじめて 1 秒間に k だけ進むのであれば,その速さは,
k ÷ 1 = k
であるかもしれません.しかし,球は,だんだん速くなります.k は,球が転がりはじめてから 1 秒間の平均の速さと言うにはふさわしいでしょうが,転がりはじめてちょうど 1 秒後の球の速さは,k より大きいと思われます.
 図 2-1-2 |
そこで,球が転がりはじめて 1 秒が経ってから,その直後のほんのすこしの時間 Δt(デルタ・ティー)のあいだに球が転がる道のりを求めて,そのあいだの速さを求めましょう.転がりはじめてから 1 + Δt 秒後までに球が進む道のりは,
| x | = k (1 + Δt)2 | |
| = k {1 + 2Δt + (Δt)2} | ||
| = k + 2kΔt + k (Δt)2. |
この値から,1 秒後までに進んだ道のり k をひくと,球が転がりはじめて 1 秒後から 1 + Δt 秒後までの t 秒間に球が進んだ道のりは,
2kΔt + k (Δt)2.
この道のりを,それを進むのにかかった時間 Δt でわると,
2k + kΔt.
これは,球が転がりはじめて 1 秒後から 1 + Δt 秒後までの平均の速さであり,わずかな Δt 秒間においても,球はだんだん速くなります.しかし,Δt が 0.1,0.01,0.001,⋯ と0に近づくにつれて,時間 Δt のあいだに生じる速さの増加量が 0 に近づきます.つまり,2k + kΔt が,転がりはじめて 1 秒後の球の速さに近づきます.そのことと並行して,Δt が 0 に近づくにつれて,2k + kΔt の値は 2k に近づきます.そのことを「Δt が 0 に近づくとき,2k + kΔt の極限(limit)は 2k に等しい」と言い,
| lim Δt→0 | (2k + kΔt) = 2k |
 図 2-1-3 |
| k (t + Δt)2 − kt2 | |
| = | kt2 + 2ktΔt + k (Δt)2 − kt2 |
| = | 2ktΔt + k (Δt)2. |
この道のりを,それを進むのにかかった時間 Δt でわると,
2kt + kΔt.
Δt が 0 に近づくとき,
| lim Δt→0 | (2kt + kΔt) = 2kt. |
つまり,転がりはじめて t 秒後の球の瞬間の速さは 2kt です.さきほどわたしたちは,転がりはじめて 1 秒後の球の瞬間の速さを求めて,2k という値を得ました.それは,いま求めた 2kt に t = 1 を代入することによっても得られます.t = 2,3,4,⋯ を 2kt に代入すると,転がりはじめて 2秒後,3秒後,4秒後,⋯ の球の瞬間の速さは,それぞれ 4k,6k,8k,⋯ です.
球が斜面を転がっているあいだ,その位置は,時間が経つにつれて変化します.その速さもまた,時間が経つにつれて変化します.では,1 秒ごとに速さが増える量は,どうでしょうか.転がりはじめて 1秒後,2秒後,3秒後,4秒後,⋯ の球の瞬間の速さは,それぞれ 2k,4k,6k,8k,⋯ です.速さは 1 秒ごとに 2k ずつ増えます.k の値は,斜面の傾きのみによって決まるので,ひとつの斜面で球を転がす場合,2k は定数です.わたしたちは,さきに運動量保存の法則について考察したさい,明白な変化の前後で,系の運動量が変化しないことを見ました.いまここでわたしたちは,球が斜面を転がる運動で,2k が変化しないことを見ています.
ここで言う比例定数 k は,斜面の傾きが大きくなるにつれて,大きくなります.斜面を地面に垂直にすると,球は真下に落下します.物体が,なににも触れないで落下する現象を,自由落下といいます.物体が,斜面でなく,空気中を落下するときにも,空気の抵抗が無視できるほど小さいならば,x = kt2 という方程式が成立し,x をメートル,t を秒の単位で計ると,k の値は地球上のどこでもほぼ 4.9 です.速さが 1 秒ごとに 2k ずつ増えるという規則性は,この場合にも成立し,2k の値は 9.8 です.
わたしたちは,運動量について考察したさい,どんな系も,他の系と衝突や接触をしないかぎり,等速直線運動を保つと仮定しました.ところが,斜面を転がる球はだんだん速くなるので,その運動は等速直線運動でありません.球が接触しているのは斜面だけですが,斜面のはたらきによって球の速さが増しているとは考えづらい.さらに,自由落下において,球は空気以外のなにものとも接触しておらず,空気の影響を無視してもなお,球の速さは時間につれて増えます.球の運動量を変える,斜面でも空気でもない原因があると,わたしたちは考える必要があります.
その原因について考察するために,わたしたちはここで,「微分(differentiation)」,「加速度(acceleration)」というふたつの語を議論に導入しましょう.
わたしたちはさきほど,球が進む道のりを表す x = kt2 という方程式から,転がりはじめて t 秒後の,球の瞬間の速さを表す式を求めました.わずかな時間 Δt 秒のあいだに球が進むわずかな道のりを Δx とすると,
| Δx | = k (t + Δt)2 − kt2 | |
| = kt2 + 2ktΔt + k (Δt)2 − kt2 | ||
| = 2ktΔt + k (Δt)2. |
これを Δt でわって,
| Δx | = | 2ktΔt + k (Δt)2 | |
| Δt | Δt | ||
| = | 2kt + kΔt. |
Δt が 0 に近づくと,上の式の極限は,
| lim Δt→0 |
Δx | = | lim Δt→0 |
(2kt + kΔt) | |
| Δt | |||||
| = | 2kt. | ||||
このようにして,転がりはじめて t 秒後の,球の瞬間の速さが得られました.このような手順で瞬間の速さを求める方法を,微分法といいます.いまの例では,道のり x を時間 t について微分しました. をひとまとめにして と表すことがあります.デルタ Δ はギリシャ文字のアルファット Α,Β,Γ,Δ,Ε,⋯ の四番目の文字の大文字で,ローマ字でいう D に相当します.「差(difference)」の頭文字が d なので,Δ や d が用いられます.Δx や Δt は,0.1 や 0.01 のように,0 に近くて,いくらと言える量を表します.一方, の dx や dt は,0 に近すぎて,いくらと言おうとしても言えない(もし言おうとすると,0.0000000000⋯ ときりがない)ものを表しています.
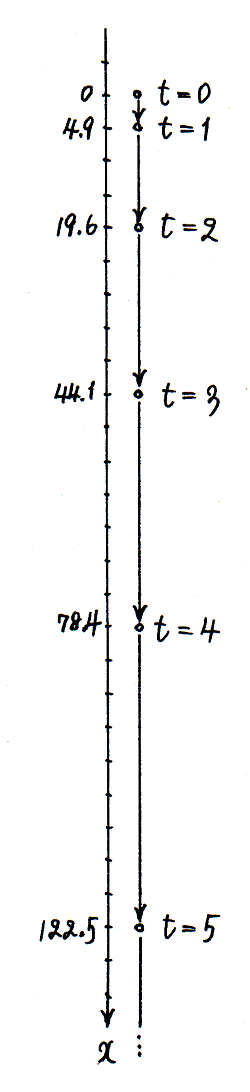 図 2-3-1 |
球の位置 x を時間 t について微分します.
| dx | = | lim Δt→0 |
Δx | |
| dt | Δt | |||
| = | lim Δt→0 |
k (t + Δt)2 − kt2 | ||
| Δt | ||||
| = | lim Δt→0 |
kt2 + 2ktΔt + k (Δt)2 − kt2 | ||
| Δt | ||||
| = | lim Δt→0 |
2ktΔt + k (Δt)2 | ||
| Δt | ||||
| = | lim Δt→0 |
(2kt + kΔt) | ||
| = | 2kt. | |||
x を,道のりでなく数直線上の位置と見なすとき,こうして得られた 2kt は,速さでなく速度です.この例で,下方に動く物体の速度は正の数で表されますが,もし上方に動く物体があるならば,その速度は負です.
速度(velocity)を v と表すと,v = 2kt という方程式が得られます.球の速度 v を時間 t について微分します.
| dv | = | lim Δt→0 |
Δv | |
| dt | Δt | |||
| = | lim Δt→0 |
2k (t + Δt) − 2kt | ||
| Δt | ||||
| = | lim Δt→0 |
2ktΔt | ||
| Δt | ||||
| = | 2k. | |||
このように,速度を時間について微分して得られる量を,わたしたちは加速度(acceleration)と呼ぶことにします.それは,単位時間(たとえば 1 秒)あたりに速度が増える量です.もし速度が減るならば,加速度は負の数で表されます.球が斜面を転がる現象で,斜面に平行に x 軸を設定すると,加速度 2k は,斜面の傾きのみによって決まる定数です.自由落下で,さきほどのように下方に伸びる x 軸を設定すると,加速度は 9.8 という定数です(距離をメートル,時間を秒で計った場合).
 図 2-4-1 |
まず,衝突説にこだわってみましょう:自由落下において,物体は他の物体と衝突している;ただし,衝突する相手の物体が,人間の目に見えない,あるいは,知覚できない,と仮定します.
わたしたちが渦動説について触れたとき見たように,かりに,地球のまわりに,人間に知覚できない渦があって,それが,球が落下する原因であるとします(1-6. 素朴な運動量で地球の公転を説明できるか).もし落下する球と同等の重さをもつ物体が,地面に平行に進んできて球に衝突するならば,それは,球の頂部,つまり球のうちもっとも高いところにある点で,球に衝突しなければなりません.そうでなければ,球は,真下でなく,地面にたいして斜めに落下することでしょう.一度や二度ならば,渦を成す物体が偶然に球の頂部に衝突するかもしれません.しかし,球が落下しているあいだずっと,渦を成す物体が球の頂部だけに衝突しつづけると仮定するのは,合理的でありません.渦を成す多数の物体が地面に平行なあらゆる方向から球に衝突すると仮定すると,球が斜めに落下するおそれを解消できます.しかし,それでもなお,渦を成す多数の物体が球の上半分だけに衝突するという非合理的な仮定を置かなければ,球が落下する現象を説明できません.
図 2-4-2 |
 図 2-4-3 |
 図 2-4-4 |
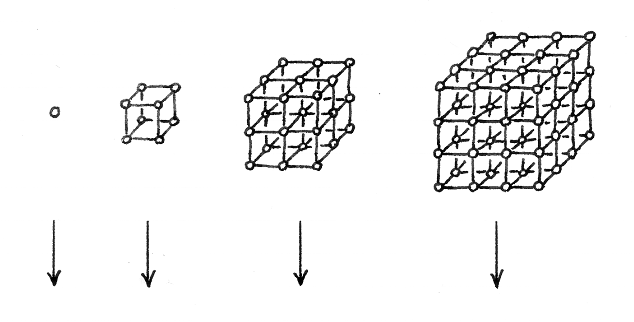 図 2-4-5 |
では,衝突説を諦めたあと,球が落下する原因として,わたしたちはなにを想定すればいいでしょうか.わたしたちは,その原因がなにであるかを知りませんが,その特徴についていくつかの推測を行うことができます.
まず,球を落下させる原因は,球の質量に比例する量であるはずです.わたしたちはここでまた,アイザック・ニュートンの意味で<原子>という語を用い,物体の質量とは,その物体を成す<原子>の個数であると定義します.ガリレオ・ガリレイが発見し,わたしたちもまた見たように,自由落下において,質量の大きい物体も小さい物体も同じように落下します.それは,物体を落下させる原因が,物体を成す各々の<原子>に同じように影響を与えるからであると考えられます.各々の<原子>が受ける影響がたがいに等しいならば,物体を成す<原子>の個数が 2 倍,3 倍,4 倍,⋯ になるにつれて,物体を落下させる原因の量は 2 倍,3 倍,4 倍,⋯ になります.つまり,物体を落下させる原因の量は,その物体の質量に比例します.
次に,球を落下させる原因は,加速度となんらかの関係があるかもしれません.わたしたちはさきに,明白な変化が起こっているにもかかわらずその前後で変化しないもののひとつが,運動量であることを見ました.自由落下においては,加速度が,明白な変化をとおして変化しません.ふたつの物体の衝突の前後でなぜ運動量の和が変化しないかをわたしたちが理解したように,自由落下で加速度が変化しない原因をもしわたしたちが理解できるようになれば,物体の運動についてのわたしたちの知識は新たな相に入るでしょう.しかし,わたしたちは,それがなぜであるかをいまの段階で説明することができません.
そしてもうひとつ.わたしたちは,物質の不可侵性(impenetrability)という前提を疑う必要があるかもしれません.ひとつの位置に,複数の物体が同時に存在することができるでしょうか.いや,ひとつの位置に複数の物体が近づいたならば,やがてそれらはぶつかって弾きあうだろう.そう考えるとき,どんな瞬間にもひとつの位置を占めることができる物質はただひとつである,という物質の性質を不可侵性といいます.それを自明な前提としているかぎり,わたしたちは,以下のような難点に直面するでしょう.
わたしたちの目に見えるほど大きな,つまり,わたしたちが感知できるほど大きな物体は,多数の<原子>がひとつのかたまり(mass)を成しています.自由落下においては,どんな球も,質量の多寡にかかわらず,同じように落下します.それはなぜか.球を落下させる原因が,球を成すどの<原子>にも均等に影響を及ぼすからであると,わたしたちは考えています.
 図 2-4-6 |
ところで,もし<原子>になんらかの大きさがあって,かつ,<原子>に不可侵性があるならば,球の外周部にある<原子>に比べて,かたまり(mass)の内部にある<原子>に,他の物質は影響を与えにくいのではないでしょうか.球を落下させる原因が,物質から成る(material)ものであるとすると,それもまた<原子>から成るはずです.その原因が球の内部にある<原子>に影響を及ぼすためには,球を成す<原子>と<原子>との隙間を,球を落下させる原因である他の<原子>が通りぬけなければならないのでしょうか.かりにそうだとすると,<原子>の隙間を通りぬけられずに弾きかえされる<原子>があるのではないでしょうか.もしいくつかの<原子>が弾きかえされるならば,球の外周部にある<原子>と内部の奥深いところにある<原子>とにたいして,落下させる原因が均等に影響を及ぼすことができません.つまり,質量の多寡にかかわらず,どんな球も同じように落下するという現象を,わたしたちは説明できなくなります.
一方,もし<原子>が幾何学的な点であるならば,球を落下させる原因である<原子>は,球を成す<原子>に,どのように影響を及ぼすのでしょうか.どの<原子>の体積もゼロであるならば,ふたつの<原子>が衝突することはありません.ふたつの<原子>がある程度近づいたとき,両者はなんらかの影響を及ぼしあう,という仮説を立てればいいかもしれませんが,もしそうであるならば,それらが影響を及ぼしあう機構は,幾何学的な点のふるまいだけでもはや説明がつきません.物質から成るものはすべて<原子>から成るという前提を変更してまで,ふたつの<原子>に影響を及ぼす,<原子>でないなにものかという存在を,わたしたちは想定すべきでしょうか.よほどの理由がないかぎり,そういうことをするのはためらわれます.
このような難点に直面するとき,わたしたちは,物質の不可侵性という前提を検討すべきであると思われます.そもそも不可侵性は,固体を念頭においたぎこちない仮説であり,気体や液体について考えるときには実用的でありません.液体である水と液体であるエタノールとが接触したら,それらふたつの物質は,弾きあわず,溶けあいます.そして,<原子>そのものは,固体でも液体でも気体でもありません.ふたつの<原子>がぶつかると弾きあうかどうか,わたしたちには判断するすべがありません.ただ,たとえ不可侵性を斥けたとしても,わたしたちの当面の困難がすべて解決されるわけではありません.かりに,ふたつの<原子>がひとつの位置で重なりあうことができるとします.そして,球を落下させる原因である<原子>が,球の外周部にある<原子>と重なりあって,それになんの影響も及ぼすことなく,それを通りぬけることができるとします.すると,球を落下させる原因である<原子>は,どのようにして球の内部にある<原子>に影響を与えるのでしょうか.さっき外周部の<原子>を通りぬけたばかりの<原子>が,なぜ内部の<原子>を通りぬけないのか,わたしたちには分かりません.
わたしたちはここでいったん,この議論を中断しなければなりません.
地球上で落下する球についての議論を離れて,わたしたちは,太陽のまわりを公転する惑星について考察しましょう.いまからしばらくのあいだ,わたしたちは数学の表現を利用します.わたしたちがいまから目指す結論に数式なしで到達するには,あまりに膨大な準備が必要だからです.人類のなかで,数式を用いずに独力でそこに到達できる者は,もしかすると今後もアイザック・ニュートンただひとりであるかもしれません.わたしたちが使おうとしている数学は,高校で習う水準のもの(楕円の方程式,三角関数の導関数,合成関数の導関数など)ですが,数式が苦手なかたはその部分を眺めるだけにしておいてください.
ルネ・デカルトは,『哲学原理』で,次のような自然の三法則を提示しました:
これらのうち第二法則に関連して,デカルトは次のように述べています.その内容は,今日の観点では誤りですが,向心力の存在がそこで示唆されています.
しばしば複数の異なる原因が同時に同一の物体にはたらくことがあり,ある原因が別の原因の効果を妨げることがある.したがって,わたしたちは,考察する原因によっては,物体が同時に異なる方向に動こうとしていると言わざるをえない.たとえば,E を中心にして振りまわされる投石器 EA 内の石 A は,もしわたしたちが運動を決定するすべての原因を考慮するならば,A から B に行こうとする.なぜならば,石は実際にその方向に行くからである.しかし,石自体にある動く力だけに注目すると,上に述べた法則[第一法則]にしたがって,石が点 A にあるとき,それは C のほうへ動こうとしている(もちろん,直線 AC は円に点 A で接する直線であるとする).というのは,かりに石が L から点 A に到達したまさにその瞬間に投石器から放りだされたとすると,石は A から,B でなく実際に C に行くであろうからである.投石器は,そのような結果を妨げているが,だからといって石がそのように動こうとするのを妨げることはできない.もしわたしたちが,石のすべての動く力に注目するのでなく,投石器によって阻止されている部分に注目するならば,そして,実際の結果をもたらすすべての力から投石器が阻止している力を区別するならば,結局,石が点 A にあるとき,石は D のほうへ動こうとしているとわたしたちは言わざるをえない.言いかえれば,石は,直線 EAD に沿って中心 E から遠ざかろうとしている.
図 2-5-1
『哲学原理』三部五十七節の図『哲学原理』三部,五十七節
まず,この記述が誤っていることを確認しましょう.投石器が石に及ぼす影響を,石が受けるそれ以外の影響から区別するならば,投石器による影響は,石を半径の方向に外に向かって動かそうとすることであると,デカルトはここで主張しています.彼は,今日の語でいう遠心力に言及していると考えられます.わたしたちは遠心力についてまだなにも考察していませんが,遠心力は,上の場合,石そのものにはたらく力でありません.わたしたちは,遊園地の乗りものに乗って遠心力を感じることがありますが,それは,乗りもの自体にはたらく力でなく,乗っている人間にはたらくように見える見かけの力です.デカルトは,遠心力が石自体にはたらくかのように述べていて,その点が誤りです.また,この節に付けられた図(図 2-5-1)も,誤解を招きかねません.その図では,投石器に拘束された石が点 A から点 B に移る運動が,拘束がない場合の点 A から点 C に移る運動に対応しているかのように,点線が描かれています.しかし,もしそのようにふたつの運動が対応すると理解するならば,石が勢いあまって中心のまわりを一周する運動を,わたしたちは説明できません.
デカルトが記したこの節でわたしたちが見過ごせない点は,手と石とをつなぐ投石器が,石の軌跡の半径であることです.石が運動する方向は,たえず変化しています.たとえ速さが一定であるとしても,方向が変化するならば,運動が変化していると,わたしたちは理解しています.では,この場合,運動を変える原因はなにか.デカルトによれば,物体の運動を変化させる原因は,その物体が他の物体と衝突あるいは接触することですから,ここで石の運動を変化させている原因は,投石器が石に接触していることです.投石器は,石を,回転の中心方向に引いています.円弧に沿って運動している物体にたいして,円の中心方向にはたらく力を向心力といいます.さきにわたしたちが,惑星の公転を,惑星と物体との衝突によって説明できるかどうかを検討したとき(1-6. 素朴な運動量で地球の公転を説明できるか),惑星に比べて衝突する物体がとても軽いならば,それらの物体は,惑星に衝突するまえに,公転軌道の中心方向に運動していることを見ました.そのことは,円に沿って運動する惑星にたいして,軌道の外から向心力がはたらくことを示しています.一方,ここでデカルトが挙げている投石器の例で,円弧に沿って運動する石にたいして,向心力は軌道の内側からはたらいています.
物体が円運動をしているとき,その中心方向になにが起きているかを,数学の手法を用いて分析しましょう.
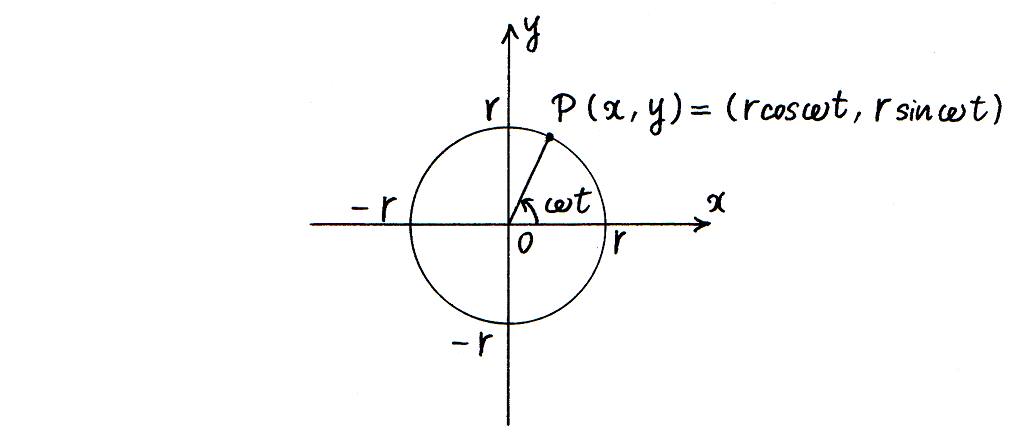
xy-座標平面上に,原点を中心とする半径 r(r > 0)の円を考え,その円上を一定の速さで動く点 P の,時刻 t における座標 (x, y) を,
(x, y) = (rcosωt, rsinωt)
とします.ω は角速度といって,点 P が単位時間(たとえば 1 秒)に進む弧に対応する中心角を表します.
x,y をそれぞれ時間 t について微分すると,
.
これらを,それぞれもういちど時間 t について微分して,
| ∴ | = | ||
| = | . |
位置 (x, y) を時間 t について微分して得られる は速度であり,速度を時間 t について微分して得られる は加速度です.点 P の加速度を a とすると,
a = −ω2 (x, y).
円の中心に太陽があり,点 P が公転する惑星であるならば,惑星の加速度は太陽のほうを向いていると,この式は示しています.物体が一定の速さで円周に沿って運動しているならば,その運動の原因によらず,物体の加速度は円の中心があるほうを向いています.言いかえれば,たとえ惑星に次々に小さな物体が衝突することによってであろうとも,たとえ惑星と太陽とが紐で結ばれていることによってであろうとも,あるいは,たとえそれ以外のどんな原因によってであろうとも,惑星が一定の速さで円周に沿って公転するならば,惑星の加速度は円の中心があるほうを向いています.
デカルトは,惑星の公転軌道が円であるという前提で議論していましたが,それは観測された事実に反していました.ティコ・ブラーエの観測記録をもとにヨハネス・ケプラーが行った分析によれば,火星の公転軌道は楕円でした.ケプラーは,自らの分析にもとづいて,惑星の公転について次の三法則を提唱しました.
ケプラーが『新天文学』で第一,第二法則を発表したのは 1609 年,『世界の調和』で第三法則を発表したのは 1619 年であり,デカルトの『哲学原理』が出版されたのは 1644 年ですから,デカルトは,ケプラーの法則を知っていながら,それらを無視したようです.惑星の軌道が円でなく楕円であるというケプラーの結論は,デカルトにとって受けいれがたいほど奇妙に思えたのでしょう.
デカルトと対照的に,ロバート・フックを含む英国ロイヤル・ソサイエティーの会員たちは,ケプラーの法則と向かいあいました.彼らのうち何人かは,1680 年代までに,惑星に逆二乗力がはたらいていると考えていました.わたしたちはさきに(1-6. 素朴な運動量で地球の公転を説明できるか),軽い物体が次々に惑星に衝突するという仮定のもとで,惑星に逆二乗力がはたらいているという結論を導けそうであることを,いったん見ました.そのときわたしたちは,距離が 倍(k は正の実数)になると大きさが k2 倍になる力を,逆二乗力といいました.それは,距離を r とすると大きさが に比例する力と言いかえられます.こんどは,ケプラーの第三法則を用いて,逆二乗力に迫りましょう.
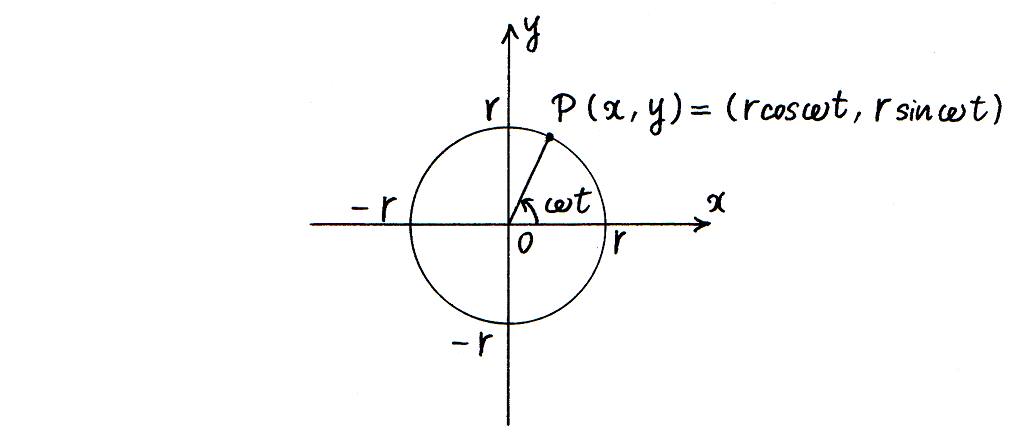 図 2-5-2 再掲 |
簡単のために,惑星の軌道が円であるとします.さきほどと同じように,半径 r の円上にある点 P の,時刻 t における座標 (x, y) を,
(x, y) = (rcosωt, rsinωt)
とします.
ですから,惑星の加速度 a は,
a = −ω2r (cosωt, sinωt).
惑星の速度を v とすると,単位時間あたりの惑星の運動量 mv の増分は,
| = | |||
| = | |||
| = | . |
その大きさは,
| = | |||
| = | . |
角速度 ω は,点 P が単位時間あたりに進む弧に対応する中心角です.一周の円に対応する中心角は弧度法で表すと 2π ですから,点 P が円を一周するのに要する時間(周期)を T とすると,
.
惑星の軌道が半径 r の円であるならば,ケプラーの第三法則より,r3 は T2 に比例します.
r3 ∝ T2. (「∝」は比例を表す記号)
上式に を代入して,
r3 ∝
両辺に をかけて,
ω2 ∝
この式の両辺に mr をかけて,
mω2r ∝
つまり,惑星の公転軌道が円であるならば,単位時間あたりの運動量の増分の大きさ mω2r は,軌道半径 r の二乗に反比例します.
わたしたちはいま,逆二乗力(大きさが に比例する力)に迫ろうとして,単位時間あたりの運動量の増分の大きさが に比例するという結論を得ました.また,さきほど(一定の速さで円運動する物体の加速度を計算する),惑星の加速度は太陽のほうを向いているという結論が得られました.物理にお詳しいかたはお気づきのように,ニュートンの言う力は,加速度に比例し,かつ,単位時間あたりの運動量の増分に比例します.しかし,わたしたちはここでも先を急がないでおきましょう.
わたしたちは,ケプラーの法則を見たばかりです.その第一法則は,惑星の軌道が,円でなく楕円であると主張しています.そのことは,なんらかの前提から推論によって導かれた結論でなく,観測によって確かめられた事実です.わたしたちは,惑星の軌道を円と仮定せずに,ケプラーの法則に向きあわなければなりません.
ロイヤル・ソサイエティーの会員であったエドモンド・ハリーが(彼は「ハレー彗星」に名が残る科学者です),そういった疑問について意見を求めるためにアイザック・ニュートンを訪問したところ,彼はすでに答えをもっていたといわれています.つまり,ニュートンは,ひとりでそれらのことを考察したうえで,他のだれも思いつかなかったいくつかの結論を持っていた,と.
ニュートンがもっていた結論のひとつは,ケプラーの法則に背いて公転軌道を円であると仮定しなくても,ケプラーの第一,第二法則から,惑星の加速度が太陽のほうを向いていることが分かる,というものでした.
楕円の方程式を,
( 0 < b < a )
とします.この楕円上を動く点 P の座標 ( x, y ) は,媒介変数 θ を用いて,
( x, y ) = ( acosθ, bsinθ ) ( θ は実数)
と表されます.
この楕円のふたつの焦点の座標は,
( −, 0 ), ( , 0 )
です.ケプラーの第一法則によれば,これらのどちらかに太陽があります.ここでは,( −, 0 ) に太陽があるとします.もし太陽がもう一方の焦点にあるならば,以下の議論に出てくる図を,紙を透かして裏から見てください.
太陽が xy-座標平面の原点に来るように,楕円を x 軸方向に だけ平行移動します.移動後の楕円の方程式は,
であり,点 P の座標 ( x, y ) は,
です.
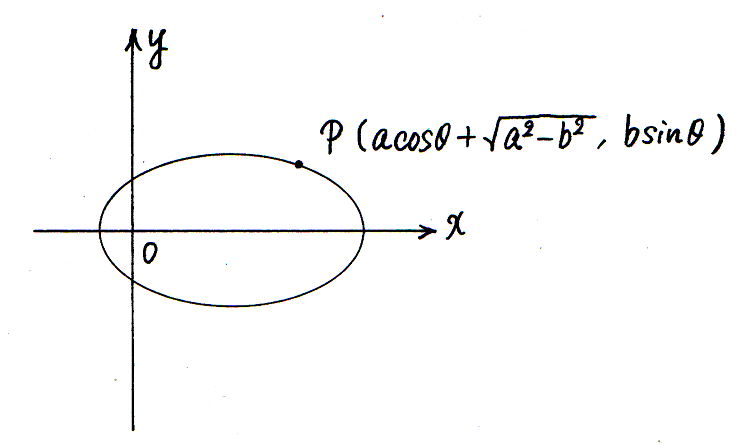
x,y をそれぞれ時間 t について微分して,
.
点 P の速度を v,速さを |v| とすると,
| v | = | . | |
| |v| | = | ||
| = | . |
θ は媒介変数なので, が正であるようにも負であるようにも設定できますが,ここでは簡単のために,惑星が動くにつれて θ が増すように θ を設定し, とします.このとき,
.
一方,点 P における,楕円 の接線の方程式は,
.
原点とこの接線との距離を h とすると,
| h | = | ||
| = | . |
太陽と惑星とを結ぶ線分が掃く面積とは,図 2-7-2 の斜線部の面積をいいます.
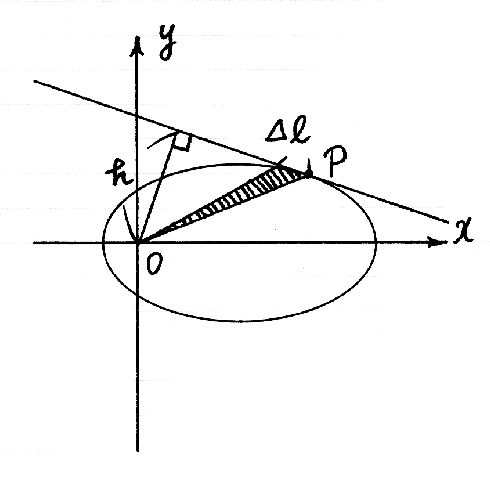 図 2-6-3 |
わずかな時間 Δt のあいだに惑星が進む道のりを Δl とすると,そのあいだに太陽と惑星とを結ぶ線分が掃く面積 ΔS は,三角形の面積 にほぼ等しい.
なので, は,
にほぼ等しい.ここで, ですから,
| = | |||
| = | |||
| = | |||
| = | . |
ひとつの惑星が公転軌道のどこにあっても の値は一定であると,ケプラーの第二法則は主張しています.そこで, (C は定数)とすると,
∴ .
この式の両辺を時間 t について微分すると,
| = | |||
| = | |||
| = | . |
これを用いると, より,
| = | |||
| = | |||
| = | |||
| = | |||
| = | |||
| = | |||
| = | . |
同様に, より,
| = | |||
| = | |||
| = | |||
| = | |||
| = | |||
| = | |||
| = | |||
| = | . |
惑星の加速度を a とすると, ですから,
| a | = | ||
| = | |||
| = | . |
ですから,惑星の加速度 a は, に平行であり,かつ,P から O のほうを向いています.つまり,惑星の加速度 a は,太陽のほうを向いています.
また,
| = | |||
| = | |||
| = | |||
| = | |||
| = | |||
| = |
| = | |||
| = | |||
| = | . |
とすると,
.
つまり,惑星の加速度の大きさは,惑星と太陽との距離 r の二乗に反比例します.
いったん,ここまでの議論を整理しましょう.
ちなみに,ニュートン自身は,『自然哲学における数学的諸原理』で,これらのことを,数式を用いず,幾何学の手続きで示しました.わたしたちがさきほど用いた微分の手続きは,ニュートン自身が発案者のひとりであり,かりに彼の時代にそのような数式が発表されたとしても,それらを理解できるひとはほとんどいなかったことでしょう.
さて,公転する惑星の加速度がゼロでない以上,その運動量はたえず変化しています.では,その運動量を変える原因は,いったいなんでしょう.ここで,わたしたちは,大胆な仮説を導入しましょう.惑星の運動量を変える原因がなんであるかについて,わたしたちは,まだ手がかりさえつかんでいませんが,なんらかの原因がとにかく存在すると仮定します.そして,その原因によって,惑星の加速度が太陽のほうを向くように決められ,同じ原因によって,その加速度の大きさが,惑星と太陽との距離の二乗に反比例するように決められると仮定しましょう.その原因を,わたしたちは「力(force)」と呼ぶことにしましょう.
わたしたちがここでどれほどの飛躍をしようとしているか,確認しておきましょう.わたしたちが議論に導入しようとしている「力(force)」は,物質から成る(material)のか,そうでないのか,わたしたちには分かりません.惑星の運動量を変える「力(force)」の源泉がもし太陽であるならば,「力(force)」はどんなしくみによって太陽から惑星に伝わるか.そのことも,わたしたちには分かりません.ルネ・デカルトが,「力(force)」のような得体のしれない存在に頼らず,衝突説に固執したのは当然でした.彼は,この世界を成す実体は「物」と「魂」とのふたつであると断定した哲学者だったからです.アイザック・ニュートンは,そのどちらでもないかもしれない「力(force)」を想定して,物体の運動を説明しようとしました.というのは,数多くの現象が,「力(force)」によって説明されるからです.
 図 2-7-1  図 2-7-2 |
さきほどの,地球上で自由落下する球について,ふたたび考えましょう.太陽のまわりにある惑星に力がはたらいているのであれば,地球のまわりにある球にも力がはたらいているはずです.力が惑星にはたらくことによって,惑星の加速度は次のように定められます:加速度の方向は,惑星から見て太陽のある方向と一致し,加速度の大きさは,惑星と太陽との距離の二乗に反比例するように.わたしたちはさきほど,xy-座標平面上で,太陽はその原点にあるとしました.もっとも,太陽には大きさがあって,それは点でありません.そこで,太陽の中心が原点にあると解釈しなおしましょう.地球のまわりにある球に力がはたらくならば,球の加速度は次のように定められるでしょう:加速度の方向は,球から見て地球の中心がある方向と一致し,加速度の大きさは,球と地球の中心との距離の二乗に反比例するように.
これらのことは,地球上における球の自由落下で見られる現象を説明できるでしょうか.加速度の方向が,球から見て地球の中心がある方向と一致する,とは,球がまっすぐに落下するということです.そのことは,自由落下で見られる現象に符合します.では,加速度の大きさが,球と地球の中心との距離の二乗に反比例するとは,どういうことでしょうか.わたしたちがさきに自由落下について見たとき,落下する球の加速度は一定であるという結論を得ました.一方,もし加速度の大きさが,球と地球の中心との距離によって変化するならば,高いところから低いところへ落下する球の加速度は一定でないでしょう.わたしたちは,そのことを次のように解釈することができます.地球の半径は 6,400 km にすこし足りない程度です.地表のふたつの地点の高低差が 100 m であったとしても,ふたつの地点と地球の中心との距離は 0.0016 %(百万分の 16) ほどしか違いません.距離を二乗して逆数をとっても,違いは 0.0032 %(百万分の 32)程度です.そのくらいのわずかな違いは,ガリレオの時代の技術で検出できませんでした.自由落下において加速度が一定であるという見解は,落下する球に上記のような力がはたらいているという説明にかならずしも矛盾しません.理論的には,球が地面に近づくにつれてその加速度は増えますが,その変化は容易に検出できるほど大きくありません.わたしたちは,惑星にはたらくのと同種の力が,落下する球にはたらいていると見なして,議論を続けましょう.
こんどは,落下する球にはたらくのと同種の力が,惑星にはたらいていると考えましょう.わたしたちは,自由落下について考察したとき,落下する球の運動量を変える原因は,球を成す各々の<原子>に均等に影響を与えると見なしました.言いかえれば,球の運動量を変える原因の量は,球の質量に比例すると見なしました.いま,わたしたちは,運動量を変える原因を力(force)と呼んでいます.つまり,自由落下する球にはたらく力(force)の大きさは,球の質量に比例すると,わたしたちは見なしています.そのことを惑星に適用すると,惑星にはたらく力(force)の大きさは,惑星の質量に比例します.力が,惑星を成す各々の<原子>に均等にはたらくからです.ただし,惑星の内部の奥深くにある<原子>が,どのようにしてその外周部をすりぬけてそこに届くのか,わたしたちは知りません.分からないまま議論を進めています.
惑星と球とに同種の力がはたらいているとすると,それにもかかわらず,惑星が楕円に沿って太陽のまわりを公転し,球が地球の中心に向かって落下するのは,なぜでしょうか.ニュートンによれば,公転と落下とは,同じ原因によって生じる現象です.地球上の高い山の頂上からボールを投げると,それはどこかに着地します.投げだすときのボールの速さを増すにつれて,ボールはだんだん遠くに着地します.やがて,投げだすときのボールの速さがある値(およそ 7,900 m毎秒)を越えると,ボールは着地するまえに地球のまわりを一周しおえます.そのボールは,その後も地球のまわりを公転します.ボールが着地する場合でも,公転する場合でも,ボールにはつねに,地球の中心がある方向に力がはたらいています.そのようにして,わたしたちは,地上にある物体の運動も,天空界にある惑星の運動も,力(force)によって説明できます.惑星の運動を理解しようとしてわたしたちが導入した力(force)は,離れているふたつの物体の一方(惑星,ボール)の運動を説明するのに役立つことが分かりました.
ところが,力(force)には姿も形もありませんから,どういう場合に物体に力がはたらいていると言うかを定義しないと,混乱が生じかねません.わたしたちは,運動量について議論したとき,どんな系も,それが他の系と衝突しないかぎり,その運動量 mv は保存されると考えていました.しかし実際には,自由落下において球はだんだん速くなり,それにともなってその運動量の大きさは増加します.また,物体が曲線に沿って運動しているならば,たとえその速さが一定であったとしても,その運動量はたえず変化していることを,わたしたちはさきに見ました.それらの場合に,球や惑星の運動量を変える原因がなんであるか分からないまま,わたしたちはそれを力(force)と呼んでいます.そこで,物体の運動量が変化しているとき,その物体に力がはたらいていると,わたしたちは言うことにしましょう.
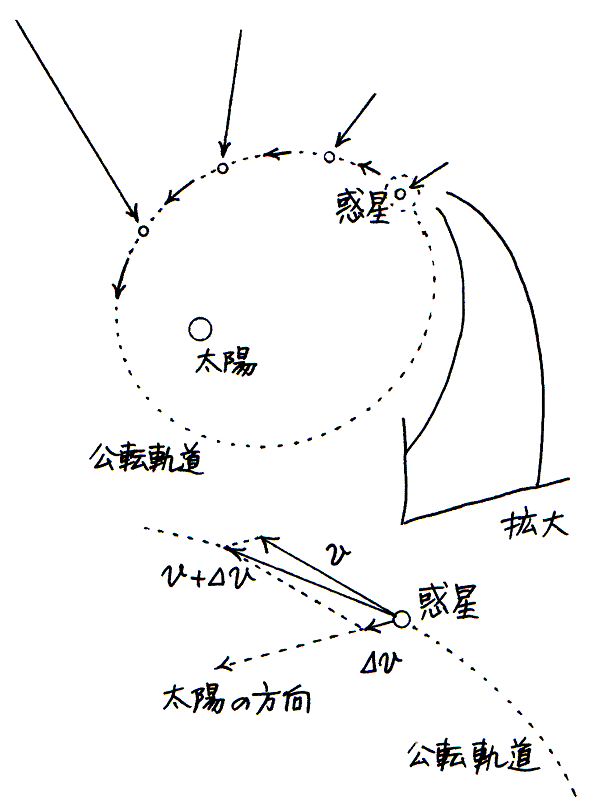
次に,わたしたちは,力の方向をどのように定義すればいいでしょうか.さきに見たように,公転する惑星の加速度はつねに太陽の中心がある方向を向いていますし,自由落下する球の加速度はつねに地球の中心がある方向を向いています.惑星の加速度が太陽のほうを向いているのに,惑星が太陽のほうへ進まないのは,なぜでしょうか.わずかな時間 Δt のあいだに速度が Δv だけ増したとき, を加速度とわたしたちは呼んでいます.地球上の自由落下でその大きさはほとんど一定でしたが,公転する惑星の加速度は時間 t とともに変化します.速さが時間 t とともに変化する場合に を瞬間の速さと呼んだのと同じように,加速度が時間 t とともに変化する場合, をわたしたちは瞬間の加速度と呼ぶことができます.加速度は,時間 Δt と速度の増分 Δv とによって決まり,もとの速度 v と直接の関係がありません.速度 v で公転している惑星の速度が,わずかな時間 Δt のあいだに Δv だけ変化するとき,太陽の方向を向いているのは Δv です.一方,惑星は,v + Δv の速度で進み,楕円の軌道を描きます.かりに軽い粒子が惑星に衝突するという説に従って説明するならば,それは,軌道の外から太陽に向かって飛んでいる途中の粒子が惑星に衝突することによって生じる現象であるということになるでしょう.いまわたしたちは,粒子の衝突によって公転が生じるという説を放棄して,公転を力(force)によって説明しようとしています.太陽の方向に飛んでいる粒子が惑星に衝突するという主張を力(force)による説明に置きかえると,惑星にはたらく力(force)は,太陽の中心がある方向を向いていると,わたしたちは言うべきでしょう.そこで,力の方向は加速度の方向と一致すると,わたしたちは定義しましょう.自由落下で球にはたらく力は,地球の中心がある方向にはたらきます.
さらに,わたしたちは,力の大きさをどのように定義すればいいでしょうか.さきに見たように,惑星にはたらく力は,惑星を成す各々の<原子>に均等にはたらきますから,力の大きさは,惑星の質量に比例します.また,力は,運動量を変える原因ですから,運動量が大きく変化するとき大きい力がはたらいていると,わたしたちは見なしましょう.加速度 a が大きいときには,速度の増分 Δv が大きいので,運動量 mv が大きく変化します.わたしたちは,力の方向が加速度の方向と一致すると見なしていますから,力の大きさもまた,加速度の大きさに応じて変わると見なしましょう.ただし,両者が比例するのか,一方が他方の二乗に比例するのか,もっと複雑な関係にあるのか,いまの段階でわたしたちには分かりません.
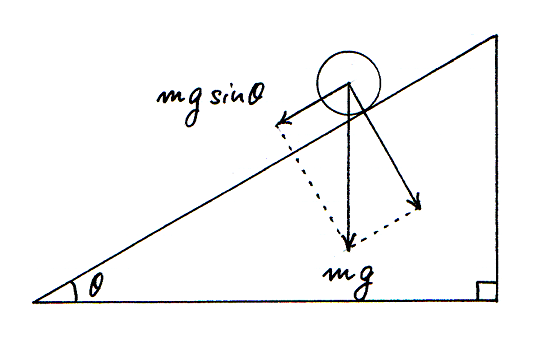 図 2-7-5 |
力の大きさが加速度の大きさに比例することは,次のような実験で確かめられます.水平面と θ の角をなす斜面を球が転がるとします.斜面と平行な方向に球にはたらく,重力の分力の大きさは mgsinθ です.さまざまな θ の値にたいして球を斜面に沿って転がし,その実験から算出される加速度の大きさと,理論上得られる mgsinθ の値とを対照すると,両者は比例していることでしょう.けれど,わたしたちの議論は,まだ「重力の分力」を扱えるまでに至っていません.
ここでは,かりに,力の大きさが加速度の大きさに比例するとしましょう.すると,次の結論が導かれます.
力の大きさは,運動量 mv を時間 t について微分した量の大きさに比例します.わたしたちは,力の大きさが質量 m に比例することを,さきに見ました.さらにわたしたちはいま,力の大きさが加速度 a の大きさに比例すると仮定しています.つまり,力の大きさが ma の大きさに比例すると仮定しています.運動量 mv を時間 t について微分すると,
| = | |||
| = |
力の大きさは,いくらの比例定数で の大きさ,あるいは ma の大きさに比例するでしょうか.それは,力,質量 m および速度 v をはかる単位によって異なります.わたしたちは,力がなんであるか知らないので,その大きさをどんな単位ではかるべきか分かりません.そこで,わたしたちは,力を f として,それが に比例する比例定数を,簡単のために 1 としましょう.そのことを表す方程式は,
あるいは,
です.
物理にお詳しいかたにとって,これらの方程式は,ニュートンによる運動の第二法則を定式化したものにほかならないでしょう.しかし,わたしたちはいま,惑星と太陽と,そして落下する物体と地球とのような,離れているふたつの物体のあいだにはたらく力について考察しているにすぎません.ふたつの物体が衝突する現象を,わたしたちは力で説明することができるでしょうか.
 図 1-5-7(再掲) |
わたしたちは,ふたつの物体が衝突する現象に「力」を持ちこみましょう.質量 mA,mB のふたつの物体が一直線上を同じほうへ進んでいて,それらの速度がそれぞれ vA,vB であるとします.やがて質量 mA の物体が mB の物体に衝突し,その後の速度がそれぞれ vA',vB' に変わるとします.衝突をとおして,これらふたつの物体から成る系の運動量は保存されます.
mAvA + mBvB = mAvA' + mBvB'.
この衝突をとおして,質量 mA,mB の物体の運動量はそれぞれ,
mAvA' − mAvA,mBvB' − mBvB
だけ増加します.ただし,運動量が減る場合,増加量は負の値で表されます.
いまわたしたちは,物体の運動量を変える原因は,物体にはたらく力であると考えています.ふたつの物体が衝突するさい,それらが接触しているわずかな時間 Δt のあいだ,質量 mA,mB の物体にそれぞれ大きさ fA,fB の力がはたらくとします.ここでは簡単のために,fA,fB の大きさが時間 Δt をとおしてそれぞれ一定であるとします.ここでもまた上の例と同じように とすると,fA,fB は,それぞれの物体の,単位時間あたりの運動量の増分です.つまり,時間 Δt をとおした運動量の増分は,それぞれ fAΔt,fBΔt です.このような「力」と「時間」との積を,わたしたちは力積(impulse)と呼ぶことにしましょう.力積は,運動量の増分を表します.
fAΔt = mAvA' − mAvA
fBΔt = mBvB' − mBvB.
これらの式の両辺をそれぞれ加えて,
fAΔt + fBΔt = mAvA' +mAvB' − mAvA − mAvB.
運動量保存の法則より,mAvA + mBvB = mAvA' + mBvB' ですから,これを上式に代入して,
| fAΔt + fBΔt | = | (mAvA + mBvB) − mAvA + mBvB | |
| = | 0. |
なお,ふたつの物体が,衝突のさいちゅうも,たとえば完全な球形を保っていると仮定すると,衝突が継続する時間 Δt はゼロであるとわたしたちは見なさなければならないことでしょう.すると,ふたつの物体がなんらかの大きさの力積 fΔt を得るさい,はたらく力 f の大きさは無限大であると言わざるをえません.むしろ,衝突のさいちゅう,どんな物体も歪んでいるとわたしたちは考えるべきでしょう.
 図 2-8-1 |
では,ふたつの物体が衝突しない場合に,ふたつの物体にはたらく力のあいだにどんな関係があるでしょうか.太陽,惑星の質量をそれぞれ M,m として,わずかな時間 Δt のあいだにそれぞれの速度が V,v から V',v' に変化するとします.わたしたちは,太陽と惑星とをひとつの系と見なしましょう.Δt をとおしてその系の運動量は保存されますから,
MV + mv = MV' + mv'.
わずかな時間 Δt をとおして,太陽,惑星にはたらく力をそれぞれ F,f とすると,運動量の増分はそれぞれ FΔt,fΔt に等しいので,
FΔt = MV' − MV
fΔt = mv' − mv
| ∴ | FΔt + fΔt | = | MV' + mv' − MV − mv |
| = | 0 (∵ MV + mv = MV' + mv'). |
つまり,力が惑星にはたらいているとき,同じ大きさ(絶対値)の力が太陽にはたらいています.惑星にはたらく力は太陽の中心がある方向を向いていましたから,太陽にはたらく力は,惑星の中心がある方向を向いていると推定されます.つまり,それらのふたつの力は,太陽の中心と惑星の中心とを通る直線上にあって,逆を向いています.惑星にはたらく力の大きさが惑星の質量 m に比例したのと同じように,太陽にはたらく力の大きさは,太陽の質量 M に比例します.力は,太陽を成す各々の原子に均等にはたらくからです.太陽と惑星とにはたらく力の大きさ(絶対値)は等しいので,それは Mm に比例します.
また,惑星にはたらく力の大きさは,惑星の加速度の大きさに比例します.ということは,両者にはたらく力の大きさは,太陽の加速度の大きさにも比例するでしょう.太陽,惑星の加速度の大きさをそれぞれ A,a とします.ところが,両者にはたらく力の大きさは,それらの積 Aa に比例しません.F = MA ですから,F が 2 倍,3 倍,4 倍,⋯ になるにつれて,A は 2 倍,3 倍,4 倍,⋯ になります.また,F = MA,f = ma,F = −f ですから,A が 2 倍,3 倍,4 倍,⋯ になるにつれて,a もまた 2 倍,3 倍,4 倍,⋯ になります.ですから,F が 2 倍,3 倍,4 倍,⋯ になるにつれて,積 Aa が 22 倍,32 倍,42 倍,⋯ になります.つまり,F は Aa に比例しません.F は,A にも a にも比例しますから,それは MmA にも Mma にも比例します.しかし,惑星にも太陽にも等しい大きさの力がはたらいているのに,A と a との一方だけが現れる式は,改善の余地を残しています.公転する惑星の加速度 a の大きさは,惑星と太陽との距離 r の二乗に反比例することを,わたしたちはさきに見ました.ですから,惑星と太陽とにはたらく力の大きさは,r2 に反比例する,または に比例します.太陽と惑星との距離 r は両者に共通の量ですから,加速度 A,a のどちらか一方を式にもちこむより,r をもちこむほうが合理的です.
惑星と太陽とにはたらく力の大きさは,両者の質量の積 Mmに比例し,両者のあいだの距離の二乗 r2 に反比例します.つまり,それらの力の大きさ f は, に比例します.さきほど,f が ma に比例するさいの定数をわたしたちは 1 と定めたので,こんどは別の比例定数を用いなければなりません.それを G とすると,
.
物理に詳しいかたはお気づきのように,これは,万有引力の法則を表す方程式です.この方程式を得るために,ここまでわたしたちが真であると見なしてきたことは,次のとおりです.
|
→ |
|
↘ | |||||||
|
→ |
|
↗ | |||||||
| → |
|
↗ | |||||||
| → |
|
↗ | |||||||
これらの根拠には,多くの形而上学的洞察が含まれています.それらの多くは,直観にもとづいていると思われます.つまり,それらを支えるさらなる根拠は存在しません.それらの洞察は,天空界の惑星の運動と符合するだけでなく,ガリレオ・ガリレイが地球上で行ったさまざまな実験とも矛盾しませんが,だからといって,いくつかの既知の現象にあとから理屈をこじつけたというそしりを免れるわけではありません.惑星の公転と落体の運動とのほかに,力で説明できる現象はないでしょうか.
 図 2-8-2 |
ここで,わたしたちは,潮の満ち干に注目しましょう.ニュートンによれば,落下と公転とは本質的に同じ現象です.詳細に見れば,落下する物体の,地球に近い部分に大きい力が,遠い部分に小さい力がはたらいています.もし物体が,落下でなく,公転していても,そのことは同じです.
また,ニュートンによれば,地球のまわりを公転する物体に力がはたらくとともに,地球にも力がはたらきます.公転する物体が,月であるとしましょう.地球の,月に近い部分に大きい力が,遠い部分に小さい力がはたらきます.
 図 2-8-3 |
地球表面の大半は海に覆われていますから,月に近い部分の海水に大きい力がはたらき,遠い部分に大きい力がはたらきます.その結果,海水のうち,月に面している部分は,地球のそれ以外の部分より大きい力で引かれて,地球の中心からすこし遠ざかります.言いかえると,海の,月に面している部分は,そのまわりの部分に比べて盛りあがります.一方,海水の,月と反対側にある部分にはたらく力は,地球のそれ以外の部分にはたらく力より小さいので,他からとりのこされて,地球の中心からすこし遠ざかります.言いかえると,海の,月と反対側にある部分もまた,そのまわりの部分に比べて盛りあがります.つまり,海の,月に面している部分と,月の反対側にある部分とは,それ以外の部分に比べて盛りあがります.地球は 1 日ごとに 1 回ずつ自転しますから,地球表面にたいして静止している観測者は,1 日にほぼ 2 回ずつ,満潮を経験します.
 図 2-8-4 |
ニュートン以前のだれも,その現象をうまく説明できませんでした.だからといって,そのことによって,ニュートン以前に知られていたことがくつがえされたわけでありません.
月や地球の部分ごとにはたらく力の大きさが異なるならば,月や地球は厳密な球形を保っていないと推測されますが,ニュートンの時代の技術でその歪みを検出することはできませんでした.
さて,わたしたちはここまで,落下する物体に力がはたらいているなどと言うにとどめて,その力を及ぼしているものがなにかについて触れていません.太陽のまわりを公転している惑星には,惑星と太陽との距離の二乗に反比例する大きさの力が,太陽の中心がある方向にはたらきます.惑星にその力を及ぼしているものが太陽であるかどうかを,論理的に決めることはできません.一方,わたしたちは,惑星に力がはたらくと見なした段階で,論理によって決められる限界を踏みだしていました.つまり,わたしたちは,力がなにから成るか,それがどのように伝わり,どのように物体にはたらくかを知らないまま,力が存在すると仮定しています.そこで,わたしたちは,もう一歩進んで,惑星に力を及ぼしている主体は太陽であると見なしましょう.同様に,太陽に力をおよぼしている主体は惑星であると見なしましょう.
「太陽が惑星に力を及ぼしている」と言ったところで,そのときなにが起きているかについて,これまでより詳細な知識がわたしたちにもたらされるわけではありませんが,それにもかかわらず,わたしたちはいくつかの利点を得ます.わたしたちはさきほど(惑星が太陽のまわりを公転する現象で,両者にはたらく力の向きは逆きで,それらの大きさは等しい),公転する惑星にはたらく力 f と太陽にはたらく力 F とのあいだに,
F = −f
という関係が成立することを見ました.いま,それらの力の動作主をそれぞれ太陽,惑星であると言うことによって,わたしたちはその関係を次のように表現できます:
わたしたちはそれよりさきに(ふたつの物体が衝突する現象で,両者にはたらく力の向きは逆きで,それらの大きさは等しい),ふたつの物体が衝突する現象でも,同様のことが成立することを見ました.質量 mA,mB であるふたつの物体をそれぞれ A,B とし,それらが衝突するさいにそれらにはたらく力をそれぞれ fA,fB とすると,
つまり,ふたつの物体が離れているか触れあっているかにかかわらず,わたしたちは次の結論を得ます:
物体 A が物体 B に力を及ぼすならば,物体 B は物体 A に力を及ぼす.それらのふたつの力の向きは逆であり,大きさは等しい.
このことを,作用反作用の法則といいます.
わたしたちが,力という観念を,そのぎこちなさにかかわらず受けいれようとしている目的は,力という観念で,運動の変化を説明することです.もしわたしたちが静止している物体について考察しているならば,そもそも で定められる力など考案する必要がありませんでした.ところが,いったん力という観念を受けいれると,わたしたちは新たな疑問に直面します:静止している物体に,力ははたらいているでしょうか;もしはたらいているのであれば,その物体はなぜ静止を保っていられるのでしょうか.
 図 2-9-1 |
たとえば,箱が机のうえで静止しているとします.そのとき,地球は箱を引いていないのでしょうか.かりに机が急になくなったとしたら,箱はただちに落下しはじめることでしょうから,地球はたえず箱を引いていると考えられます.では,机のうえの箱ははぜ落下しないのでしょうか.
それは些細な問いであり,簡単に答えられると思うかたがいるかもしれません:箱が落下しようとしても,机が行く手を邪魔していて,箱は落下できない;だから箱は静止しているしかない,と.たしかに,わたしたちがふだんの生活を送るにあたって,それ以上の説明が求められることはめったになさそうです.しかし,それは,物体の運動は他の物体との接触(あるいは衝突)によって変化するという説明と対であるべきものです.わたしたちは,接触(あるいは衝突)に頼ることなく,力という観念によって,箱が静止している現象を説明することができるでしょうか.
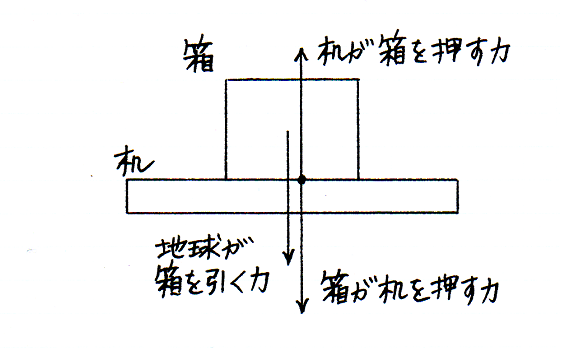 図 2-9-2 |
机から箱を取りあげて手に載せると,わたしたちは,箱が手を下向きに押していると感じます.素朴な考えでは,それは,地球が箱を引く力が手に伝わったからだと説明されるかもしれません.しかし,なんらかの力が存在するとわたしたちが見なすとき,その力を及ぼす動作主(主体)と,その力を受ける対象(客体)とを,わたしたちは明確に指ししめすことができるとしましょう.すると,「地球が箱を引く力が手に伝わる」という表現は曖昧です.その力の対象(客体)は,箱であって,手でないからです.わたしたちの考えによれば,手を下向きに押す力の動作主(主体)は,箱でなければなりません.
同じように,机のうえで箱が静止しているとき,地球が箱を引く力と別に,箱が机を下向きに押す力が存在していると,わたしたちは見なしましょう.そして,その例に,作用反作用の法則を適用しましょう:箱が机を下向きに押す力が存在するならば,机が箱を上向きに押す力が存在します.
わたしたちはいま,箱が受けるふたつの力(箱を対象とするふたつの力)を見つけました:
箱が机のうえで静止しているのは,これらの力がつりあっているからであると,わたしたちは見なしましょう.そうすることによって,箱が地球に引かれているにもかかわらず箱が静止している現象を,わたしたちは力という観念で説明できます.
このことは,混乱を招きがちです.作用反作用の法則を説明するための図と,力のつりあい(equilibrium)を説明するための図とが,似ているからです.作用反作用の法則は,物体がどんな運動をしているかにかかわらず,
物体 A が物体 B に力を及ぼすならば,物体 B は物体 A に力を及ぼす.それらのふたつの力の向きは逆であり,大きさは等しい
と主張しています.つまり,ひとつの力が,他の力と関係なく存在することはありません.力はかならず,ふたつ一組で存在します.そして,それらふたつの力の対象(客体)は異なります.
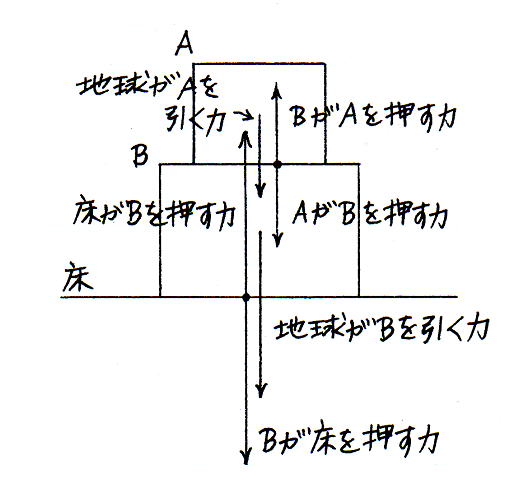 図 2-9-3 |
一方,力のつりあいは,力が物体にはたらいているにもかかわらず,なぜ物体の運動は変化しないかを説明する観念です.複数の力がつりあっているとわたしたちが見なすとき,それらの力の対象(客体)は一致します.たとえば図 2-9-3 で,A にはたらく力は,
のふたつです.それらの力が,つりあっています.「A が B を押す力」は,B にはたらく力ですから,A にはたらく力のつりあいに関与しません.「A が B を押す力」と「B が A を押す力」とは作用反作用の関係にありますが,両者の対象(客体)は異なっているので,それらの力がつりあっているわけではありません.
また,力のつりあいには,ひとつの物体にはたらくすべての力が関与するので,みっつ以上の力がひとつの物体にはたらいて,つりあっていることがあります.図 2-9-3で,B にはたらく力は,
のみっつであり,それらがつりあっています.それにたいして,作用反作用の関係ある力は,かならずふたつ一組です.
では,わたしたちは,地球が静止している物体を引く力の大きさを,どのように表せばいいでしょう.わたしたちはこれまで,力の大きさを,いくつかの方法で表してきました.
そもそも力は,物体の運動を変える原因ですから,これらの方法のなかで,力の大きさを と表すのが理にかなっています.けれど,わたしたちはいま,静止している物体にはたらく力の大きさについて論じています.物体の運動量は変化しません.
一方,地球が箱を引く力の大きさは,
(G:万有引力定数,M:地球の質量,m:箱の質量,r:地球の重心と箱の重心との距離)
と表されます.この式を用いると,静止している箱を地球が引く力の大きさは であり,その力は下向きです.その力とつりあっている,机が箱を押す力の大きさもまた, であり,その力は上向きです.この式は,正確ですが,その一方,分数がわずらわしいうえに,箱の性質によらない複数の定数を含んでいます: 万有引力定数 G はもともと定数ですし,地球上の物体にはたらく力の大きさを考察するさい,地球の質量 M は定数です;静止している物体にはたらく力の大きさを考察するさい,地球の重心と物体の重心との距離 r は定数です.そこで, を g とすると,箱にはたらく力の大きさは mg と表されます.
いまわたしたちは, をひとまとめにしたものが g であると言いましたが,力の大きさは,質量と加速度との積でも表されます.力の大きさを mg と表すならば,g は加速度を意味します.それは,もし箱が自由落下をするならば,そのときに観測される加速度です.箱が静止しているにもかかわらず,わたしたちは,箱にはたらく力の大きさを,その箱が自由落下をする場合の加速度を用いて表すことができます.
わたしたちはこの章で,アイザック・ニュートンが考案した力という観念について見ました.ここで見たいくつかのことを体系化するために,ニュートン自身は『自然哲学の数学的諸原理』で運動についてみっつの法則を提唱しました:
ニュートンが尊敬していたケプラー,そして仮想論敵であったデカルトの両人が,それぞれみっつの法則を唱えたので,彼は彼らにならったのだろうと思われます.
ニュートンによる運動の第一法則は,デカルトが『哲学原理』で提唱した,自然についての第一法則と実質的に同一です.
運動の第二法則で言われている運動の変化とは,今日のわたしたちの語法で言いかえると,単位時間あたりの運動量の増分です.つまり,物体の運動量が単位時間あたりにどれほど増加するかは,その物体にはたらく力の大きさに比例し,その運動量が増える方向は,その力の方向と一致すると,第二法則は主張しています.物体の質量を m,その速度を v,物体にはたらく力を f とすると,この法則は,
と表されます.質量 m を時間 t によらない定数と見なすと, が成立します.単位時間あたりの速度の増分 を,わたしたちは加速度 a と呼んでいますから,上式は a を用いて,
f = ma
と表されます.
第一法則は,第二法則の特殊な一例であると言われることがあります.第二法則 f = ma で,f = 0,m ≠ 0 とすると,a = 0 が得られます.このことは,物体に力がはたらいていないならば,その物体の加速度はゼロである(つまり,運動量の増分はゼロである)ことを示しています.ですから,わたしたちがいったん第二法則を受けいれたあとで第一法則を振りかえると,後者は前者の一例として説明されます.しかし,第一法則は,もし力が存在しなくても,成立します.実際,ルネ・デカルトは,ニュートンの意味での力を想定せずに,ニュートン以前にそれと同内容の法則を提唱しました.第二法則で言及されている力は,ニュートンが人類史上初めて提唱した観念であり,力がどのように伝わるか,それがなにでできているか,それはそもそも実在するかという点について,人々の疑念を招くおそれがありました.その一方,力を用いれば,わたしたちは,地上の物体の落下運動と太陽のまわりの惑星の公転とを,統一した観点から説明できます.たとえ力が存在していなくても成立する第一法則と,彼自身が考案した力を定義する第二法則とは,区別されるべきであるとニュートンは考えたと思われます.
第一法則は,慣性の法則とも呼ばれます.わたしたちはこれまで,質量を,ニュートンの意味での<原子>の個数と理解してきました.しかし,彼の意味での<原子>は,今日なお存在すると確かめられていません.そこで,ニュートン以後の科学者たちは,質量を別の意味に解釈しました.そのひとつが,質量の大きさは慣性(inertia)の大きさを表しているという解釈です.慣性は,その物体の速度が変化しにくい程度と言いかえられます.
物体にひとつの力がはたらいている場合,第二法則は,
ma = f
と表されます.また,物体に複数の力 f1,f2,f3,⋯ がはたらいている場合,それは,
ma = f1 + f2 + f3 + ⋯
と表されます.これらの式は,運動方程式と呼ばれます.
第三法則は,作用反作用の法則です.わたしたちはさきに,運動量保存の法則を用いて作用反作用の法則を導きました.逆に,作用反作用の法則から次のように運動量保存の法則を導くこともできます.
それぞれの質量が mA,mB であるふたつの物体 A,B が,一直線上をそれぞれ速度 vA,vB で運動していて,やがて衝突するとします.それらふたつの物体が接触しているわずかな時間を Δt とします.簡単のため,Δt のあいだ,A が B に一定の力 f を及ぼすとします.この力を受けているあいだの,物体 B の加速度を aB とすると,
mBaB = f
∴ .
aB は単位時間あたりの速度の増分ですから,時間 Δt が経過したあとの B の速度を vB' とすると,
| = | |||
| = | . |
一方,作用反作用の法則より,Δt のあいだ,B は A に一定の力 −f を及ぼします.この力を受けているあいだの,物体 A の加速度を aA とすると,
mAaA = −f
∴ .
衝突が終わったあとの A の速度を vA' とすると,
| = | |||
| = | . |
そこで,mAvA' + mBvB' を mA,mB,vA,vB で表すと,
| = | |||
| = | |||
| = |
この式は,運動量保存の法則です.
一方,わたしたちはさきに,ニュートンの独特の<原子>論と第一法則とにもとづいて,運動量保存の法則を導きました.そして,それをもとに,第三法則を得ました.
以上のように,ニュートンの運動の三法則は,たがいに関係しあっています.
わたしたちはいま,どんな物質も,膨大な個数の小さな<原子>から成ると考えています.そして,どんな物質を構成している<原子>も共通であると考え,その洞察をアイザック・ニュートンに帰しています.しかし,彼がたしかにそのように考えていたという,文献上の証拠はありません.
ニュートンは,『光学』(1704)で次のように記しました.
ここまでのすべてを考慮すると,私には,以下のことがありそうに思われる.神は,始めに,中身の詰まった,塊を成しやすい,割れにくい,不可侵の,可動な粒子[原文で複数形]で,物質を作った.それらの粒子の大きさ[複数]や形[複数],他の諸性質,空間にたいする比率は,神がそれらを作った目的にもっともよく適うように定められている.始めに創られたそれらの粒子は,中身が詰まっているので,それらから構成されるどんな多孔性の物体より,比べものにならないくらい割れにくい.それらの粒子は,擦りへることがなく,割れてばらばらになることがない.通常の能力では,神自身が始めの創造で一としたものを分割できない.それらの粒子が欠けることがないかぎり,それらは,いつの時代にも変わらない性質をもつ物質を構成するだろう.物質の性質は粒子に依拠しているので,かりに粒子が擦りへったり,割れてばらばらになったとしたら,その性質は変化することだろう.かりに,擦りへった古い粒子や粒子のかけらでできている水や土があるとするならば,それらの性質は,欠けることのない始めのままの粒子でできている現在の水や土のものと,同じでないことだろう.しかしそれらの性質は変わることがないだろうから,したがって,物質から成るものの変化は,それらの恒久的な粒子がさまざまに分離したり,新たに結合したり,運動することによってのみ生じうる.複合した物体が壊れやすいのは,中身の詰まった粒子のまんなかにおいてでなく,それらの粒子が集まって,わずか二,三の点で接触している箇所においてである.アイザック・ニュートン『光学』「疑問 31」より
ニュートンは,『光学』の末尾に未解明の「疑問」を列挙し,それらにたいする彼の見通しを示しました.「疑問」は 31 項に及び,最後の「疑問 31」で彼は原子論に言及しました.上に引用した段落は,「疑問 31」のわずかな一部です.「疑問 31」のそれより後方に,彼は次のように記しました.
空間はかぎりなく分割できるものであり,物質はかならずしもすべての場所に存在するわけでないから,次のこともまたあるかもしれない.神は,物質を成す粒子を,いくつかの大きさや形に創ることができ,空間にたいするいくつかの比率を定めることができ,おそらくそれらに異なる密度と力とを与えることができ,そうすることによって自然の法則を変えることができ,宇宙のいくつかの部分にいくつかの種類の世界を作ることができる.同上
この箇所でニュートンは,神が<原子>を「いくつかの(several)大きさや形」に創ることができるという見通しを述べています.わたしたちはここまで,すべての<原子>の大きさや形は同じであると考えてきましたから,ニュートンの記述はわたしたちの前提と一見異なります.しかし,彼がここで述べているのは,わたしたちの世界と異なる種類の世界についてです.そのことは,わたしたちの世界において原子が均一であるという前提に反しません.とはいえ,原子が均一であるという見解をニュートンがどこかで披露しているわけではありません.
結局のところ,わたしたちは,間接的な証拠からニュートンの<原子>観を推測するしかありません.
これらのことのいくつかは,今日の物理学を知る者に,しばしばニュートンの不可解さと映ります.けれども,彼が<原子>を均一であると見なしていたと仮定するならば,それらのいずれもが彼にとって合理的であったとわたしたちは見ることができるかもしれません.
ニュートンによる質量の定義が,密度と体積との積であることについて,わたしたちはさきに(1-7. 原子についてのニュートンの考え)見ました.
「活力論争」とは,今日の語でいう「運動量」と「運動エネルギー」とのどちらのほうが,物体の運動の大きさを表すのにふさわしいかという論争です.その論争を仕掛けたゴットフリート・ライプニッツは,今日の「運動エネルギー」にあたる量を発見し,「運動量」を推すデカルト派を論敵としました.ニュートンもまた,デカルト派を論敵としていましたが,彼はライプニッツの主張を斥けて,「運動量」を支持しました.わたしたちがさきに見たように,デカルトの言う運動量は「大きさと速さとの積」であり,ニュートンの言う運動量は「質量と速度との積」ですから,ニュートンはデカルトを追認したわけではありません.もしニュートンが均一原子論者であったならば,彼にとって,運動量は,均一原子論と慣性の法則と他のいくつかの仮説から導かれるものであり,それは,彼自身が考案した「力」にたいして論理的に先行します.
ニュートンは,『光学』の「疑問 29」で,光線は粒子から成るかもしれないという見通しを述べ,「疑問 30」で,光線と物質とは相互に転換することができるかもしれないと述べています.もし彼がそこで言っている「粒子」が,わたしたちが言っている均一な<原子>と同一のものであるならば,彼がそのように考えたのは当然です.
もしニュートンが均一原子論者であったならば,彼はまた,どんな物質もなんらかの過程を経て別の物質に変化すると考えたことでしょう.もし錬金術師が原子論を自説の根拠とするならば,その原子論は,物質の転換を説明できるものでなければなりません.ニュートンがデカルトの運動量を改変したことと,彼が錬金術師であったこととは,相容れないどころか,むしろ同一の原子論にもとづいていたということがありそうです.
ユニテリアニズムとは,キリスト教の三位一体を否定し,イエスと精霊とを神と認めない信仰の総称です.それはいわば,「創世記」で世界を創造した父なる神だけを,あるいは,それに相当する存在だけを,神と認める立場です.ニュートンは,あえて大多数のキリスト教教会の教義に背いて,そのような信仰を持っていました.そのような者にとって,一で完結する説明と多を必要とする説明とでは,前者が好ましいことでしょう.
なお,ニュートンが均一原子論者であっただろうという推測は,高校物理の教科書に載っていませんが,わたしたちに独特のものでありません.たとえば,湯川秀樹は,次のように記しました:
Newton 自身は目に見える物体を,そのまま 1 点にまで凝縮さすという,数学的極限操作を行なわなかった.その代り目に見える物体は,いかに小さくても,無数の目に見えない原子の集りであると想定したらしく思われる.そうすると,簡単のため原子はみな同じ微小物体と見なせば,単位体積内の原子の数を数えることによって,物質の密度が測られることになる.湯川秀樹『現代物理学の基礎 1 古典物理学 I』(1978)
第 2 章 運動と力とに関する諸法則
ちなみに,湯川が編集に参加した『現代物理学の基礎』シリーズでは,電磁波の媒質としてのエーテルが実在するという仮定のもとで,古典電磁気学が記述されています.正統な物理学において,エーテルの実在は 20 世紀初頭に否定されました.しかし,湯川は,誤った仮説にもとづいて正しい理論が構築されていくようすを興味深いと思ったのでしょう.「原子はみな同じ微小物体」であるという誤った仮説にもとづいて,彼が古典力学を記述することはありませんでした.わたしたちはいま,彼が考えて記さなかったことの一部と向かいあっているかもしれません.
けれど,かりにニュートンが均一原子論者であったとしても,現実の世界でそのような原子は発見されていません.わたしたちは,エルンスト・マッハの次の言葉に耳を傾けるべきでしょう:
まず,質量の概念を「物質の量」と説明する考えかたはまったく適切でないと,わたしたちは見なす.「物質の量」という概念が,十分な明晰性をもっていないからである.たとえ多くの著者たちがしてきたように,仮説上の原子の個数に戻ったとしても,そのことは変わらない.エルンスト・マッハ『力学の発展:史的かつ批判的な観点で』(1883)
第 2 章 動力学の原理の発展,5 反作用原理と質量概念との批判
マッハによれば,ふたつの物体の質量が等しいとは,次のように定義されます.
大きさの等しい反対向きの加速度をたがいに与える物体を,等しい質量の物体とわたしたちは言う.同上
マッハの言うとおりに質量を理解するならば,わたしたちは,方程式で質量を扱える一方で,質量とはなんであるかについていっさいの予断をもつことを許されません.質量を<原子>の個数と解釈することは,いわば,たとえ話のようなものであると,わたしたちは自覚しなければなりません.
(準備中)