2019 年 7 月 27 日から 8 月 11 日まで，新御徒町にある mograg gallery で開催されている「アイドルと芸術 3」。その展覧会に，O'CHAWANZ の りるはかせ がフィボナッチ数の絵を出しています。なにそれ。

フィボナッチ。人名です。いまの国でいうとイタリア人。男性。彼が著した『算盤の書』に，ネズミ算ならぬウサギ算が紹介されていて，そこに現れる数列（sequence）を後世の人々がフィボナッチ数列と呼ぶようになりました。そのウサギ算の問題は，次のようなものです：

問 どんなウサギのつがい（オス，メス 1 羽ずつ）も，次の性質を満たすとする。

• ウサギは，オス，メスのつがいを成し，生後 2 か月目に，一度，子を産む。
• 子を産んだウサギのつがいは，その後，毎月一度，子を産む。
• ウサギのつがいは，一度にちょうど 2 羽の子を産む。その一方はオス，他方はメスである。
• この問題を考えているあいだ，どのウサギも死なない。

あるとき，一組のウサギのつがいが生まれたとする。上の規則にしたがってウサギが殖えるとき，ウサギのつがいの数の推移を調べよ。

たとえば，「3 か月後」には，その月に生まれたばかりのつがいが 1 組いて，生後 1 か月以上を経たつがいが 2 組います。前者は，その翌月に子を産みませんが，後者は産みます。ですから，「4 か月後」には，その月に生まれたばかりのつがいが 2 組いて，生後 1 か月以上を経たつがいの数は 3 組になります。以下同じです。

上の表の右端の欄に並ぶ数を，フィボナッチ数といいます。

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ...

ぼくがこのウサギ算のことを初めて聞いたか読んだかしたとき，この問題の設定が理解できなかったことを覚えています。

• ウサギって，生後 2 か月で子を産むの？
• ウサギって，毎月，子を産むの？
• ウサギって，兄弟姉妹で子を産むの？
• つがいは固定されてるの？ メスとつがいになるオスは月によって入れかわるの？
• 叔母と甥，とか，祖父と孫娘，という組もあるの？

その後ぼくは，ヒュー・ヘフナーが雑誌 PLAYBOY のマスコットにウサギ（バニー）を採用した理由を知りました。ウサギは多産で好色であるという先入観が欧米文化にあって，彼はそれを利用した，と。なるほど。キツネはずるいとか，ハイエナはあさましいとか，ある種の野生動物は先入観にもとづいて語られることがあります。フィボナッチのウサギ算は，それにもとづいていたようです。それ以来ぼくは，動物園などでウサギを見かけるたび，こいつらどんだけ好色なんだろうと観察するようにしています。

「n か月後」のつがいの合計 a_n は，どのように求まるでしょうか。

• 「n か月後」に新たに生まれるつがいの数は，「(n − 1) か月後の，生後 1 か月以上を経たつがいの数」に等しい。それは，「(n − 2) か月後の，すべてのつがいの数 a_n−2」に等しい。
• 「(n − 1) か月後に生きていた，a_n−1 組のつがい」は，すべて「n か月後」にも生きている。

なので，
     a_n = a_n−1 + a_n−2
が成立します。

これ，解きましょうか？

文具の蔵 Rihei 宮洋墨 富士山湧水 Aqua Blue で記す

「フィボナッチ数はぜんぶ整数なのに，その一般項を表すのに，無理数である $\sqrt{5}$ が必要です」──と言うと，かしこそうに聞こえます。わたしも，言われたことがあるし，言ったこともあります。でも，それは，たいしてかしこくないと最近は思ってます。一辺 1 の正方形をかいたら，対角線がすでに $\sqrt{2}$ ですからね。物理学者のリチャード・ファインマンは，電磁気学の教科書（もとは講義）で，電場という概念は必要であるし，そのうえさらに実在すると，学生たちに訴えかけました。しかし，数学教師が，無理数という概念は必要であるし，そのうえさらに実在すると力説することはなさそうです。三平方の定理を習ったら，その段階で無理数は実在してます。ありがたくない。

フィボナッチ数は，黄金比に関係があります。一般項 a_n を表す式の右辺にある $\frac{1+\sqrt{5}}{2}$ が黄金比に関係あるからです。符号が 1 か所異なる $\frac{1-\sqrt{5}}{2}$ の値は，およそ，
     (1 − 2.2360679...) ÷ 2 = −0.6180339...
です。その n 乗の値は，n が大きくなるにつれて，0 に近づきます。なので，それを無視することにすれば，フィボナッチ数のおよその値は，$\frac{1}{\sqrt{5}}{\left(\frac{1+\sqrt{5}}{2}\right)}^n$ です。n 番目のフィボナッチ数の近似値 $\frac{1}{\sqrt{5}}{\left(\frac{1+\sqrt{5}}{2}\right)}^n$ に，$\frac{1+\sqrt{5}}{2}$ をかけると，(n + 1) 番目のフィボナッチ数の近似値 $\frac{1}{\sqrt{5}}{\left(\frac{1+\sqrt{5}}{2}\right)}^{n+1}$ が得られます。日本語で数学のことを考えているとそういう言いかたになりますが，欧米語で考えると，1 : 2 と 1 ÷ 2 は同じものなので，
      $\frac{1}{\sqrt{5}}{\left(\frac{1+\sqrt{5}}{2}\right)}^n$ : $\frac{1}{\sqrt{5}}{\left(\frac{1+\sqrt{5}}{2}\right)}^{n+1}$ = 1 ÷ $\frac{1+\sqrt{5}}{2}$ = $\frac{2}{1+\sqrt{5}}$ = $\frac{2}{1+2.2360679}$ = 0.6180339...
が黄金比（golden ratio）です。りるはかせは，展示作品で，「分母の有利化」と呼ばれる操作を行って，黄金比を $\frac{-1+\sqrt{5}}{2}$ と表していますが，それはここで求めたものと同じ値です。

それはそうとして，$\sqrt{5}$ の近似値 2.2360679... は，富士山麓鸚鵡鳴く（フジサンロクオームナク）と覚えます。富士山麓を賑わすアイドル Mi-II のファンには覚えやすいですね。

黄金比は美しいといわれることがあります。どうなんでしょ？

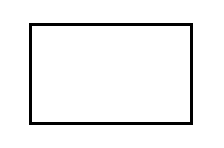
この長方形は，たてよこの比が黄金比です。他の長方形より美しいですか。感じかたはひとそれぞれですのでお任せしますが，ぼくは，とくに美しいと思いません。もし黄金比が美しいとしたら，それは見た目のことでなく，官能的なものでないとぼくは思っています。西洋絵画，とくに宗教画において，見た目の美しさ，官能美は，建前のうえで本質的なことではありませんでした。聖書の出来事などを（おもに字の読めない）信者にわかるようにすることが，宗教画の最優先課題でした。いまでいうと，「ビッグ・バンのウン秒後に宇宙はこんなようすだった」とか「Society 5.0 が実現したら暮らしはこうなる」とかを説明するイラストレーションのようなものです。見た目はぱっとしなくても，細部にまで意味が込められています。

たとえば，精神科医ジャック・ラカンは，こんなことを言っています。「私」にとっての「他者」の関係は，「神（それは，私＋他者）」にとっての「私」の関係に等しい，と。なにそれ？という疑問を尻目に，「私」を 1，「他者」を a とします。
     私 1 : 他者 a = （私＋他者 1 + a） : 私 1
     a(1 + a) = 1²
     a² + a − 1 = 0

この方程式の正の解は，
     $a=\frac{-1+\sqrt{5}}{2}$ = 0.6180339...
     神（それは，私＋他者） = $1+\frac{-1+\sqrt{5}}{2}=\frac{{\displaystyle 1+\sqrt{5}}}{{\displaystyle 2}}$

他者が黄金比で，神はその逆数です。ここでラカンがなにを言ってるのか，ぼくにはわかりませんが，それは居心地が悪くて心に残る主張です。宗教画の細部を意味で満たそうとした人々が，このような比を絵画に忍びこませたことは不思議でありません。

フィボナッチ数列には，さまざまな性質があります。りるはかせは，展示作品で，フィボナッチ数列の項の二乗の和が，隣接する二項の積に等しい，という性質をとりあげています。こういう定理を紹介すると，それはなぜかと問われることがあります。むかしはぼくもその問いを真に受けて，計算を示したりしていましたが，問われているのはそういうことじゃないと最近気づきました。それはなぜか。これとこれがカチャっとはまるとこうなるから，くらいの文字数で直観的に理解できる理由が求められているようです。しかし，残念ながら，このあたりの定理にそういう便利な説明はありません。シマウマに縞があるように，フィボナッチ数列はそういう性質をもっているとしか言いようがありません。そして，その性質を美しいと感じるひとがいます。

余談ですが，ぼくもフィボナッチ数列についての定理をひとつ自力で見つけたことがあります。フィボナッチ数列の初項から第 n 項までの和が，第 (n + 2) 項から第 2 項を引いた値に等しいというものです。自力で見つけたというだけで，第一発見者ではありませんし，なんの役にも立ちそうにない駄定理です。証明は簡単なので省略します。でもね，

初項からこつこつと第 n 項までたしあげた結果は，ふたつあとの第 (n + 2) 項に現れるのである，しかしそのさい，2 番目の項の値だけは引かれているのだ

とかね，ときどき意味ありげに言ってみたいじゃないですか。意味ないんですけど。

フィボナッチの本名はピサのレオナルド。ローマ数字 I, II, III, ... を使ってたヨーロッパ世界に，アラビア数字（算用数字） 1, 2, 3, ... と位取り記数法とをもたらした人物です。彼が富士山麓を賑わすアイドルのプロデューサーだったとしたら，Mi-2 と名付けたことでしょう。